No Monte um Computador Analógico (ART3212), ensinamos como montar um computador com potenciômetros e alguns componentes adicionais, cujo potencial de cálculo surpreendeu a muitos de nossos leitores. Nós mesmos temos o protótipo ainda montado o qual montamos num vídeo ((veja no final do artigo o link). Demos exemplos de diversos cálculos e até fizemos um curso que mostrava como usar este computador (Computação Analógica – Lição 1 – Os Computadores Analógicos (CUR6001) – Curso de Computação Analógica). Neste artigo vamos um pouco além mostrando alguns cálculos avançados que podem ser feitos com o computador analógico.
Lembramos que neste tipo de computador o funcionamento é semelhante de um ábaco, ou seja, trabalha-se com uma escala analógica contínua o que significa que a precisão está diretamente ligada ao modo como fazemos a leitura e a precisão dos componentes usados.
Como numa régua de cálculo, os resultados são aproximados e tanto mais próximo do real quanto maior a precisão dos componentes usados.
Divisão
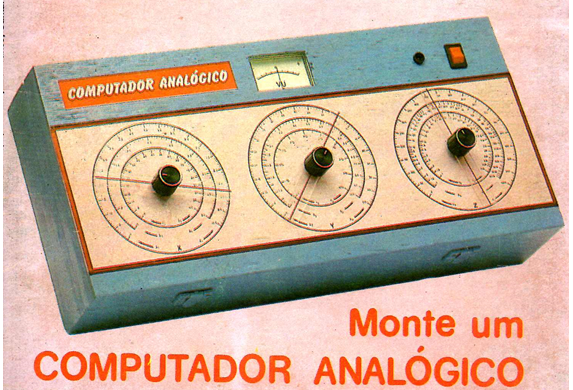
A divisão é o oposto da multiplicação. Por exemplo, se 2 X 3 é igual a 6, então 6 / 3 é igual a 2, e 6 / 2 é igual a 3. Suponha que você deseja dividir 850 por 72. Defina Z em 850 (escala externa C). Defina Y em 72 (escala externa B). Em seguida, ajuste a posição do ponteiro X até que o medidor não mostre nenhuma corrente ao pressionar o botão de leitura (que ativa o galvanômetro)
. A resposta para 850 / 5= 72 é então encontrada na escala externa do potenciômetro X. (Figura 2). Observe que a escala A em X vai de 0 a 10,0 e essa escala B em Y vai de 0 a 100. Suponha que você deseja dividir 770 por 8,9. Defina 770 em Z e 8.9 em X. Ajuste o ponteiro para Y para obter a resposta.
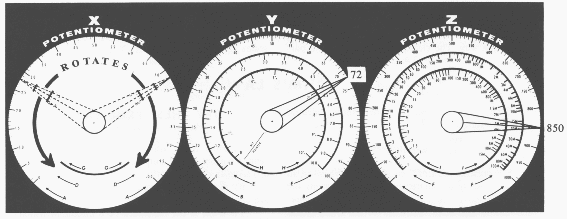
Às vezes, os números são muito grandes ou muito pequenos para a escala mostrada. Por exemplo, se você deseja dividir 8.650 por 6,5, é impossível fazer isso diretamente, porque o maior número na escala Z é 1.000.
Nesse caso, reduza o número 8.650 mudando a vírgula decimal uma casa à esquerda (dividindo por 10). Agora divida 865 por 6,5. Quando você conseguir o valor da resposta, é 1/10 da quantia adequada. Simplesmente mude o ponto decimal de volta para aumentar em 10 vezes o valor a resposta. Agora você terá a resposta correta para o problema original (8650 / 6,5).
Por meio desse recurso de deslocamento de vírgulas decimais, é possível para ajustar qualquer multiplicação ou problema de divisão para caber os números nas escalas dos mostradores.
Observe que as configurações do dial são precisas apenas cerca de dois ou três dígitos. Para um número assim como 962,4, posicione o ponteiro para a configuração mais próxima que conseguir. As respostas não serão mais precisas em 2 dígitos. A questão da precisão foi discutida em outros artigos nossos.
Resolvendo fórmulas
Uma boa quantidade de fórmulas usadas ciências e matemática são da forma X . Y = Z. Nesta fórmula, onde o ponto significa “multiplicar”. Essa fórmula também é escrita como X Y = Z, sem o ponto.
Uma forma típica deste tipo é:
A = LX
A = Área de um retângulo
L = Comprimento
X = Largura
Você, portanto, resolveria os problemas com o cálculo da área de um retângulo usando seu comprimento e largura usando a escala A, B ou C. Para fazer isso,
primeiro compare as fórmulas da seguinte forma:
XY = Z
LX = A
Observe que colocamos a fórmula para área na mesma forma que X Y = Z. Assim, se você definir a escala potenciômetro X para o comprimento de um retângulo e a escala B do potenciômetro Y como sua largura, a resposta correta para a área será encontrado na escala C do potenciômetro Z.
O comprimento e a largura podem ser invertidos sem que o resultado seja afetado. Por exemplo, 2 X 5 = 10 ou 5 X 2 = 10. Ambos equivalem. Portanto, você poderia igualmente usar a escala A no potenciômetro Y para a largura e escala B do potenciômetro Y para comprimento. Mas a área deverá permanecer no potenciômetro Z porque é o produto do comprimento e largura.
Observe que na fórmula X Y = Z existem três quantidades que variam ou mudam. Essas quantidades são, portanto, chamadas de variáveis.
Mas elas estão relacionadas sempre da forma na fórmula X Y = Z. Este relacionamento é chamado de função. Neste caso, Z é uma função de X e Y e mudará com X ou Y. O circuito elétrico é configurado para um determinada função em que Z = X Y. Como isso é feito analisamos em outro artigo desta série em que ensinamos como o computador funciona.
A seguir daremos algumas fórmulas importantes de uso comum e que são da forma X Y = Z podendo, portanto, ser resolvido com escalas A, B e C dos potenciômetros X, Y e Z.
Lei de Ohm
Não precisamos ressaltar a importância da Lei de Ohm para cálculos que envolvam eletricidade e eletrônica. A lei de Ohm estabelece que:
V = RI
Onde V é a tensão ou força eletromotriz indicada em Volts
I é a tensão dada em amperes
R é a resistência em ohm
Lei de Joule
Outra fórmula do tipo indicada é a que expressa a potência elétrica dissipada num circuito.
P = VI
Onde:
P é a potência em watts
V é a tensão em volts
I é a corrente em ampères
Exponenciação
Outra possibilidade de uso do computador analógico está no cálculo potências.
Se você multiplica o número 3 por ele mesmo, obtém: 3 X 3 ou 9. Isso também pode ser escrito como 32 = 9.
O pequeno 2 na parte superior direita de 3 é chamado de potência. Ele indica que o número à esquerda deve ser multiplicado por ele mesmo duas vezes
O que significa 34? Os matemáticos indicariam isso como 3 X 3 X 3 X 3. Resolvendo essa operação você encontrará que a resposta é 81. Assim: 34 = 81. Isso é lido como “3 elevado à 4ª potência é igual a 81”.
O segundo conjunto de números (escalas D, E e F) nos mostradores X, Y e Z permitem estimar potências de um número. Por exemplo, encontre 54 (leia, 5 elevado a 4ª potência). Isso é o mesmo que 5 X 5 X 5 X 5.
Defina a potência na escala D do potenciômetro X para o número 4.0. Defina o número 5 na escala E do potenciômetro Y (Figura 3). Gire o dial Z e encontre a resposta na escala F do potenciômetro Z quando o medidor é zerado quando você pressiona o botão.
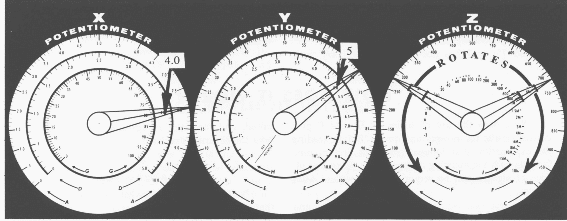
O número no dial D representa a potência. O número a ser elevado a uma potência está na escala E. A resposta é encontrada na escala F.
A resposta correta para 54 (ou 5 X 5 X 5 X 5) é 625. O ponteiro do seu computador estará próximo a este número, mas será difícil estimar com precisão.
Aviso importante: Os números na discagem F aumentem muito rapidamente, e mesmo uma ligeira mudança posição causa uma grande diferença na resposta. Por causa dos grandes erros neste processo suas respostas são estimativas aproximadas.
Estimativas deste tipo podem ser muito úteis em resolvendo um problema como este: Encontre 6.33,5. Resolução:
Defina a potência (3,5) na escala D. Defina 6,3 na escala E.
Encontre a resposta na escala F.
A resposta correta é 396. Você encontrará o ponteiro na escala F em algum lugar naquela região.
Mas você deve estar se perguntando o que é realmente 6,33,5
meios. Veja a seguir:
Raízes
No item anterior, você aprendeu que 5 X 5 X 5 X 5 (54) é igual a 625. Suponha que você foi solicitado a determinar um número cuja 4ª potência seja 625.
Você sabe que 5 é a resposta, já que 5 X 5 X 5 X 5 é igual a 625. Diz-se que o número 5 é raiz quarta de 625. Para encontrar este número com o seu computador defina o número 4 (a raiz) no dial D.
Defina 625 no seletor F e, em seguida, gire o seletor central e leia a resposta (5) na escala E. Você simplesmente inverte o procedimento para encontrar a raiz.
Os matemáticos escrevem uma raiz desta maneira x = ∜(625) Também pode ser escrito como 6251/4. A raiz segunda de um número também é chamada de raiz quadrada. A raiz terceira de um número é geralmente chamada de raiz cúbica.
Tente resolver este problema. Encontre a raiz 4ª de 7 elevado à 18ª potência. Isso significa que você deve encontrar um número que, quando multiplicado por ele mesmo 4 vezes, é igual a 7 multiplicado por ele mesmo 18 vezes. Ou isso poderia ser escrito como:∜(7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7)
Poderíamos escrever isso de forma mais simples como718/4. Os matemáticos descobriram que é possível simplificar isso ainda mais, dividindo 18 por 4, para obter 74,5.
Encontrar 718/ 4 ou 74.5 não é fácil usando a aritmética comum. Com o seu computador analógico, uma estimativa rápida pode ser obtida da seguinte forma.
Defina a potência (4,5) na escala D.
Defina o número 7 na escala E.
Encontre o valor estimado da resposta na escala F.
A resposta correta é 6.353.
Você vai encontrar sua resposta em algum lugar da escala do computador próximo disso. (Nota: para reduzir o uso de zeros na escala F, a letra M é usada para denotar mil. Portanto, 30 M significa 30 milhões)
Suponha que o problema fosse encontrar (4,5)√6,353 (encontre a raiz 4,5 de 6.353). Você simplesmente trabalha do modo inverso. Ajuste 4.5 na escala D.
Ajuste 6.353 (aproximadamente) na escala F.
Encontre a resposta na escala E (aproximadamente).
Agora tente este problema. Encontre (8,2)4,4. Ajuste 4.4 na escala D. Defina 8,2 na escala E. Encontre a resposta da maneira usual na escala F.
O que (8.2)4 4 significa? Pode significar (8,2)44/10 , (8,2)22/5 ou (8,2)88/20. Todas essas quantidades são a mesma coisa e tem a mesma resposta. Mas, por exemplo, (8.2)22/5 significa: multiplique 8,2 por si mesmo 22 vezes e, em seguida, obtenha a raiz 5ª do resultado.
Conclusão
Você deve estar surpreso com as possibilidade de cálculo com um simples computador analógico feito com três potenciômetros.
É claro que não obtemos respostas absolutamente corretas, dado o princípio de funcionamento e as tolerâncias dos componentes, mas temos estimativas para os resultados que são de grande utilidade no uso prático.
Os exemplos dados foram obtidos do manual do kit de um computador elaborado pela Science Materials Center Inc. dos Estados Unidos, vendido em 1959, mas pode ser aplicado a qualquer computador analógico do mesmo tipo.
Observamos que para o computador que descrevemos no nosso site (veja o LINK) pode haver diferenças quanto ao uso das escalas em cada um dos potenciômetros, mas o princípio de funcionamento é absolutamente o mesmo.