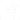Os amplificadores operacionais podem ser utilizados numa infinidade de projetos, destacando-se os de filtros ativos, que adquirem características próprias que dificilmente podem ser conseguidas com outras bases. Em especial, os amplificadores operacionais com transistores de efeito de campo na entrada se prestam à elaboração de inúmeros tipos de filtros que encontram aplicações em áudio, instrumentação, instrumentos musicais etc. Neste artigo focalizamos alguns tipos de filtros com operacionais com sua teoria básica e alguns circuitos práticos. As informações para a elaboração deste artigo foram obtidas em manuais de fabricantes como a Texas Instruments, além de outras fontes que serão citadas no final do artigo.
O que é um filtro? Partindo desta pergunta acreditamos estar atendendo a uma grande quantidade de leitores, principalmente os estudantes que necessitam de uma base mais firme para entender bem o assunto.
Podemos então definir um filtro como sendo um circuito capaz de se comportar de maneira seletiva diante de sinais de determinadas frequências.
Os filtros podem ser passa-baixas, passa-altas ou passa-faixas, conforme deixem passar os sinais de baixas frequências, altas frequências ou de uma faixa determinada, conforme o nome sugere.
As “respostas" destes filtros representadas graficamente são mostradas na figura 1.
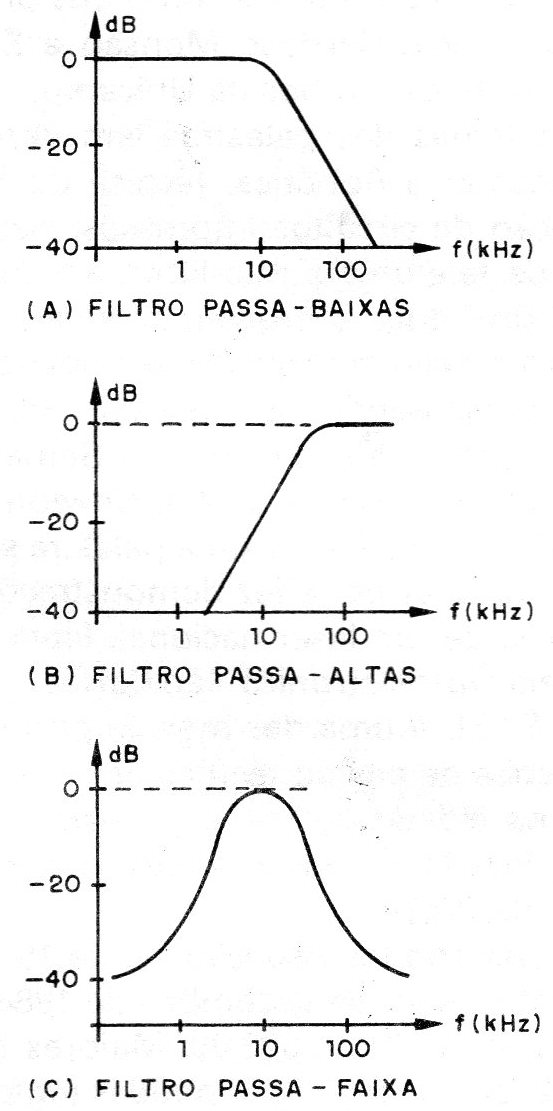
Veja que em (a), por exemplo, temos um filtro passa-baixas em que todos os sinais abaixo de uma determinada frequência, denominada "de corte", passam sem sofrer atenuação, enquanto que os demais são atenuados num grau que dependerá da ação do circuito.
Os filtros básicos são formados apenas por componentes passivos, tais como resistores, capacitores e indutores, de modo que os sinais passam sem sofrer qualquer tipo de amplificação.
Isso significa que os filtros deste tipo atenuam os sinais das frequências que não correspondam àquela faixa que devem deixar passar; estes são denominados “filtros passivos".
Na figura 2 temos alguns exemplos de filtros deste tipo.
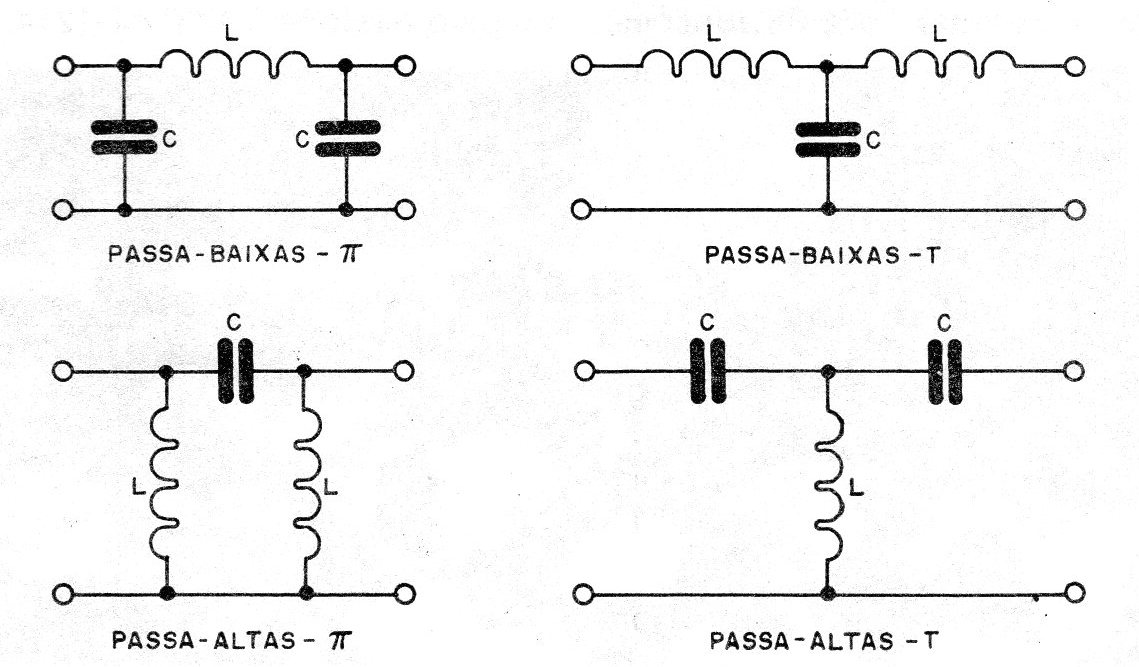
A atenuação mesmo do sinal que deveria passar sem sofrê-la, faz com que os filtros deste tipo encontrem muitas limitações nas aplicações práticas.
A combinação dos elementos de um filtro deste tipo com amplificadores operacionais acrescenta aos filtros uma propriedade importante: a de poder amplificar os sinais que correspondam a uma faixa desejada de frequência, ou pelo menos evitar que ocorram perdas num nível que impeça a sua utilização prática.
Isso nos leva a filtros que apresentam um ganho real de potência ou amplificação, e que são denominados “filtros ativos".
Num filtro ativo temos um amplificador que pode adicionar energia ao sistema, resultando ao mesmo tempo no efeito de filtragem e num ganho de potência.
Outras vantagens são apresentadas por filtros deste tipo como, por exemplo, sua baixa impedância de saída, a possibilidade de se associar diversas etapas sem perdas de potência e a capacidade de se obter funções com alto Q em baixas frequências, sem a necessidade de se utilizar indutores.
Nos circuitos de baixa frequência esta não necessidade de indutores é importante, pois estes componentes deveriam ter valores altos, resultando em peças caras e volumosas.
Conforme o tipo de circuito, os filtros podem ser projetados com características que vão de 6 a 50 dB por oitava.
Dentre as vantagens destes circuitos destacamos as seguintes:
Não há perda por inserção. O sistema pode prover ganho, se necessário.
Custo. Os componentes dos filtros ativos são mais baratos do que indutores, principalmente os de valores elevados.
Sintonia. Os filtros ativos podem ser facilmente sintonizados e ajustados numa ampla faixa de frequências sem alteração das curvas de resposta.
Isolação. Estes filtros apresentam boa isolação em vista de sua elevada impedância de entrada e baixa impedância de saída o que reduz a um valor mínimo a interação entre o filtro e a sua carga.
Damos a seguir alguns tipos de filtros que têm por base amplificadores operacionais:
FILTRO PASSA-FAIXA
Neste tipo de filtro temos a passagem de sinais de uma faixa (banda) específica de frequências, com a rejeição de sinais de todas as outras frequências que não estejam nesta faixa.
O equivalente passivo mais comum faz uso de um indutor e um capacitor (LC), no entanto, nas baixas frequências o projeto se torna difícil em vista da necessidade de grandes indutores.
O circuito ativo com operacional tem a vantagem de não necessitar de indutores.
O circuito da figura 3 é um filtro ativo de dois polos tendo por base um amplificador operacional com FET do tipo TL081.
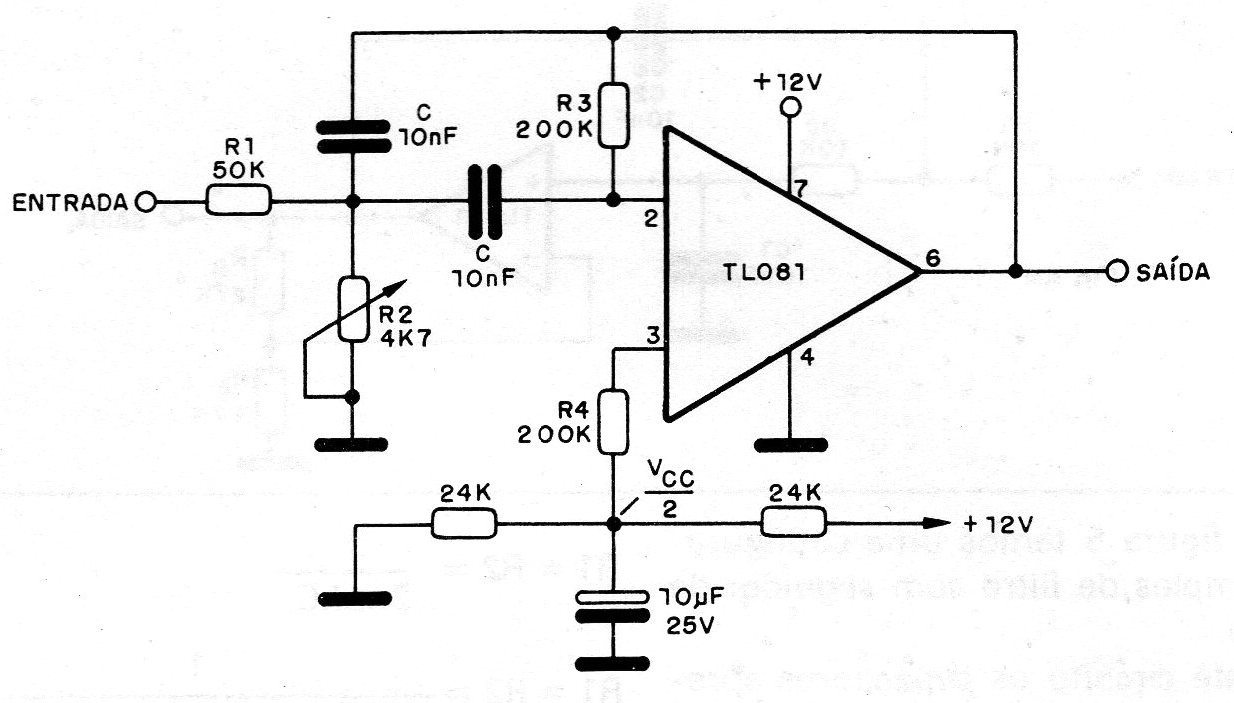
Este circuito é recomendado para aplicações que exijam fatores Q menores que 10, e o ganho é ligeiramente maior do que a raiz quadrada do fator Q.
Assim, para um fator Q igual a 5 temos um ganho da ordem de 2 vezes.
Os valores dos componentes para este filtro são calculados a partir das seguintes fórmulas:
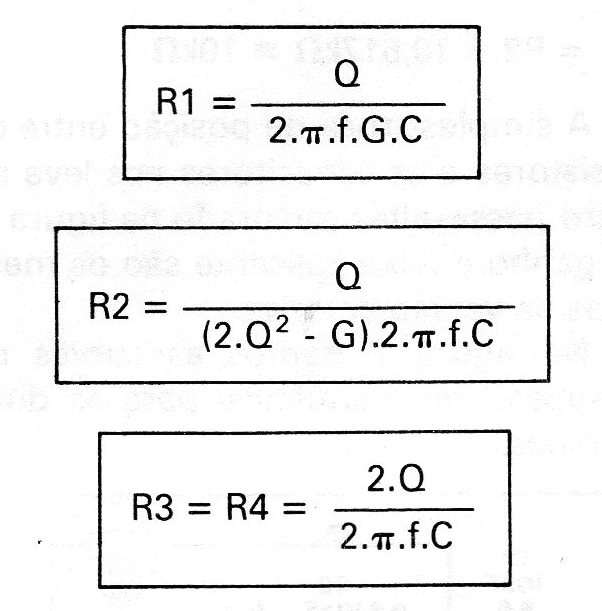
Onde:
f= frequência central do filtro (Hz)
Q == fator de qualidade
G = ganho
C = capacitância (F)
Tomemos como exemplo um filtro com frequência central de 800 Hz. R2 é um potenciômetro com duas vezes o valor calculado que permite ajustar precisamente a frequência.
Este valor maior é sugerido para compensar as tolerâncias dos demais componentes.
Para a faixa de áudio os valores dos capacitores estão tipicamente na faixa de 10 a 100 nF.
Considerando f = 800 Hz, Q = 5, G = 2 e C =1onF,temos:

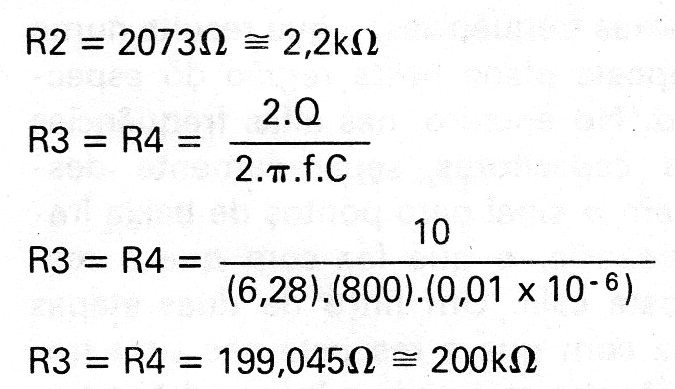
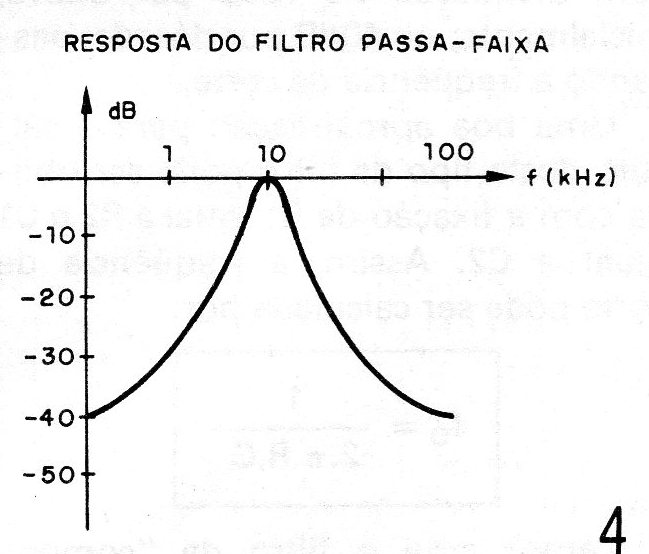
Na figura 4 temos a curva de resposta deste filtro. Esta curva tem como referência uma tensão de entrada de 4Vpp.
Filtro Passa-Altas e Passa Baixas
Dos muitos tipos de filtros que podem ser usados para deixar passar sinais somente de altas ou somente de baixas frequências, o “Butterworth" é o melhor.
Filtros complexos normalmente utilizam redes de primeira e segunda ordem.
As redes de primeira ordem não são muito úteis, porque só podemos controlar a frequência central, enquanto que nas de segunda ordem podemos, além da frequência central, controlar também a impedância e o amortecimento ou o seu inverso, o fator Q.
Na figura 5 temos uma configuração simples de filtro com seguidor de tensão.
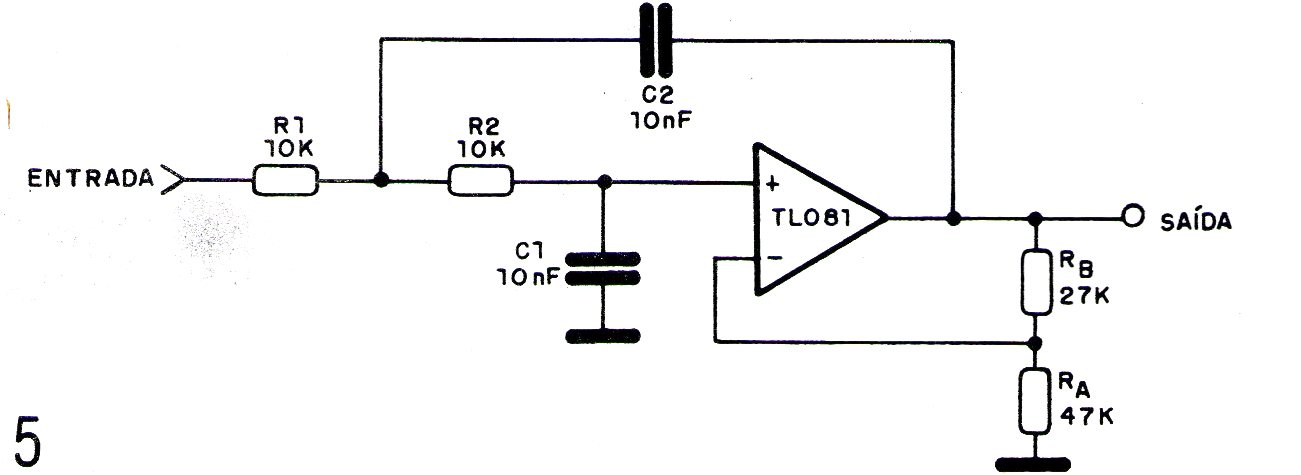
Neste circuito os capacitores apresentam um efeito muito pequeno nas baixas frequências, o que resulta numa reposta plana nesta região do espectro.
No entanto, nas altas frequências os capacitores separadamente desviam o sinal para pontos de baixa impedância, o que faz com que a resposta caia.
Um filtro de duas etapas faz com que a resposta nas altas frequências caia com o quadrado da frequência, daí o nome de filtro de segunda ordem para esta configuração.
A resposta começa plana nas frequências mais baixas para cair depois com atenuação de 12 dB por oitava, inicialmente, ou 4odB por década, passando a frequência de corte.
Uma boa aproximação para o cálculo deste tipo de filtro pode ser obtida com a fixação de R1 igual a R2 e C1 igual a C2. Assim, a frequência de corte pode ser calculada por:
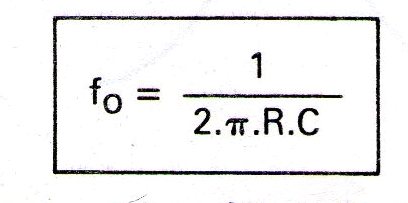
Temos aqui o filtro de "componentes iguais" com uma faixa passante de 1,586 (+4dB) para uma rede Butterworth de segunda ordem, e este é o único ganho que faz com que o circuito funcione apropriadamente.
Como o amplificador operacional opera na configuração não inversora, o resistor de realimentação RB deve ser 0,586 vezes o valor do resistor de entrada RA para um ganho de 1,586.
Para projetar um filtro passa-baixas com frequência de corte de 1500 Hz proceda da seguinte maneira:
Fixe RA em 47 Ω. RB deverá ser então RA x 0,586 ou aproximadamente 27k Ω. Se fixarmos os capacitores em 1onF os resistores serão selecionados a partir da fórmula:

A simples troca de posição entre os resistores e os capacitores nos leva ao filtro passa-altas mostrado na figura 6.
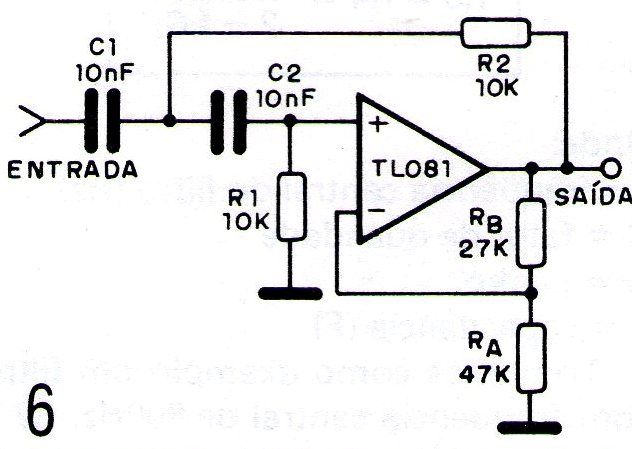
O ganho e faixa passante são os mesmos da versão anterior.
Na figura 7 damos as curvas de resposta em frequência para as duas versões.
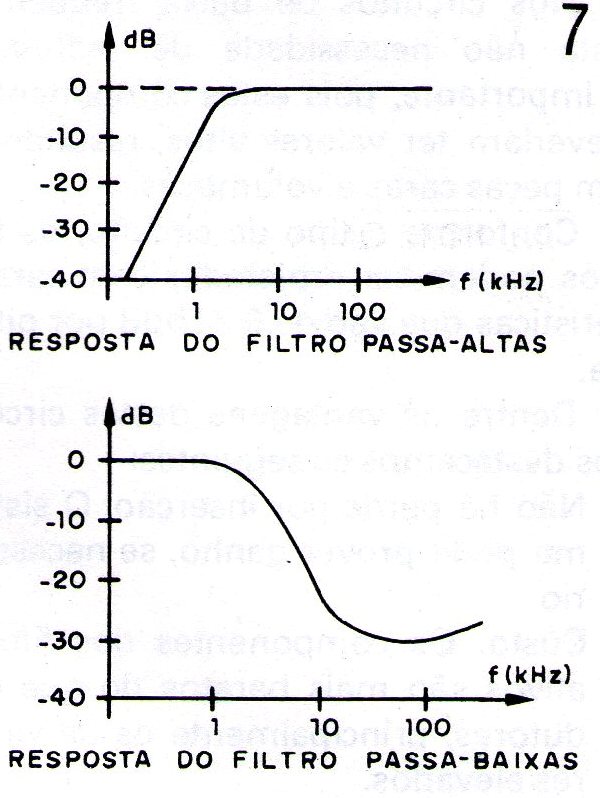
FILTRO PASSA-FAIXA COM MULTIPLA REALIMENTAÇAO
O filtro básico passa-faixa de múltiplo feedback ou realimentação é empregado quando se deseja um fator Q da ordem de15 e um ganho "moderado”.
A única dificuldade que se encontra na utilização de tais filtros é que à medida que o fator Q aumenta eles se tornam mais críticos, acentuando-se a dificuldade em fazer sua sintonia.
A experiência mostra que filtros passa-faixas ativos de alta performance e alto Q não podem ser projetados eficientemente com um único amplificador operacional.
Assim, as versões com um único operacional são indicadas para os casos em que se deseja baixo fator Q (entre 2 e 5 tipicamente).
Afortunadamente, valores nesta faixa são indicados para muitas aplicações em áudio tais como equalizadores, controles de tom etc.
Na figura 8 temos um circuito de uma única etapa de realimentação múltipla onde o amplificador operacional é ligado no modo inversor.
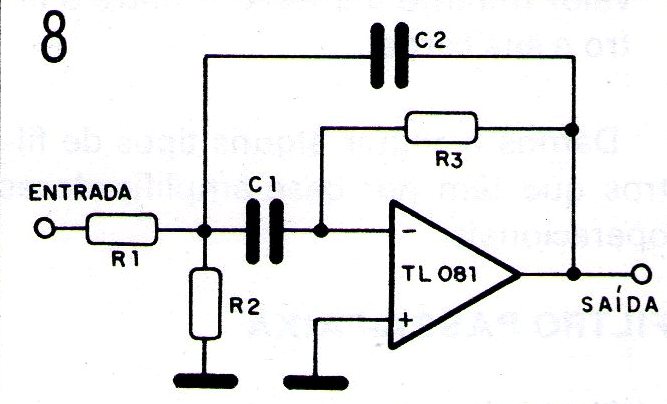
O resistor R3 da saída à entrada inversora fixa o ganho e a corrente através do capacitor C1, que determina a frequência de operação.
O capacitor C2 proporciona a realimentação da saída para a junção de R1 com R2. C1 e C2 devem ser sempre de mesmo valor.
O resistor R2 pode ser ajustável para se fazer a sintonia.
A frequência é dada pela seguinte fórmula:
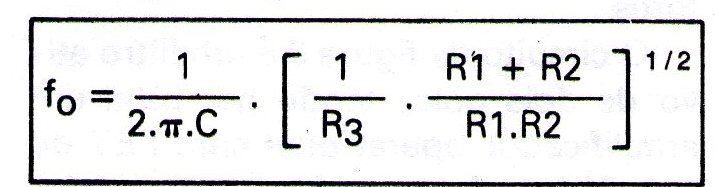
Ao projetar um filtro deste tipo parte-se de C1 e C2 com valores iguais entre 10 e 100 nF para a faixa de áudio, o que resulta em valores razoáveis para os resistores.
Vamos supor o projeto de um filtro para 10 kHz com fator Q e um ganho igual a 2.
Os três resistores são determinados da seguinte forma:

Nesta fórmula temos:
G = ganho ='2
Q = fator de qualidade = 3
C = capacitância = 1onF
f= frequência central = 10 kHz
FILTROS COM GIRÁDORES
Os giradores (gyrators) levam este nome pelo fato de seu princípio de funcionamento ter analogias com os giroscópios mecânicos.
Um girador pode se comportar como um indutor e num filtro ativo isso é importante, pois, conforme falamos no início do artigo, os indutores para baixas frequências são um impedimento para os projetos práticos em vista de seu custo e tamanho.
Uma indutância apresenta uma impedância de:

Onde:
ZL é a impedância em Ω
F é a frequência em Hertz
L é a indutância em henrys
j é o operador imaginário que equivale a raiz quadrada de -1 necessário pelo fato de haver uma rotação de fase onde a corrente adianta-se à tensão.
Para simular uma indutância precisamos de um circuito que satisfaça esta equação.
Na figura 9 temos um diagrama em blocos de tal circuito.
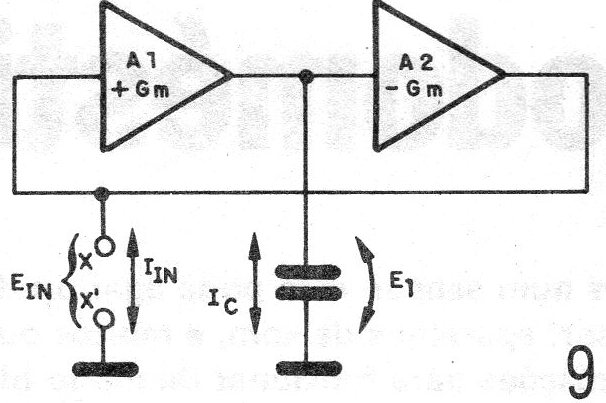
Os amplificadores A e B são do tipo operacionais de transcondutância que devem ser iguais, exceto pelo fato de que um deles inverte a fase do sinal.
Para efeito de cálculos, supondo G o ganho, temos: IGm1l = IGm2l
Para o circuito especificamente temos:
IIN = Gm.E1 (I)
ZIN = EIN/IIN (II)
EIN = -IC / Gm (III)
Substituindo as equações l e III na equação Il temos:

Substituindo a equação V na equação IV temos:

A equação VI pode ser “melhorada" se fizermos:

Rearranjando a equação chegamos então a:
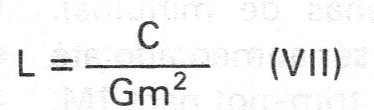
Esta equação corresponde justamente à de uma indutância, mas sem indutor! Isso mostra que tal circuito pode ser usado eficientemente para simular um indutor de qualquer valor num filtro!