Na eletrônica, em várias ocasiões, nos deparamos com equações onde os logaritmos devem ser calculados. Um exemplo muito comum é no cálculo do ganho de um sistema. Alguns sabem calcular os logaritmos e quais são suas propriedades, mas poucos entendem o conceito de logaritmo e o que significa essa ferramenta matemática.
Leia mais: Nota: Artigo publicado na revista Eletrônica Total 118 de 2006
O que são os logaritmos?
No século XVII o surgimento de matemáticos, filósofos e físicos era grande. Novas teorias nasciam a todo o momento. Johannes Kepler (1571 —1630), com suas teorias das órbitas dos planetas, era um destes filósofos-matemáticos. Ele se deparou com equações exponenciais, grandes e de resolução complexa. A capacidade de cálculo da época e as ferramentas matemáticas existentes não permitiam a rápida resolução dessas equações, o que tornava esses cálculos um verdadeiro martírio.
Neste ambiente, John Napier (1550 — 1617), escreveu uma obra que revolucionou a matemática e permitiu a solução dessas equações complexas em muito menos tempo e de modo muito mais simples. Seu principal livro foi o "Mirifice Logarithmorum Canonis Descriptio" (1614), cuja tradução seria "Uma maravilhosa descrição das leis da evolução". Sim, o conceito de logaritmo desenvolvido por Napier mostra a evolução de um número para outro número. Como assim?
Ao começar a calcular números exponenciais, Napier percebeu uma propriedade implícita. Veja por exemplo potências utilizando a base 10, mostradas na equação 1:

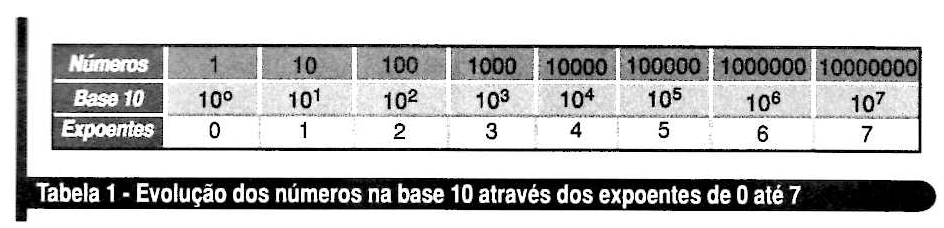
Note que o expoente 1 resulta no número 10, o expoente 2 resulta no número 100, o expoente 3 resulta no número 1000, e assim por diante. Pensando desta maneira, Napier organizou os números de um modo diferente, como a mostra a tabela 1.
Napier observou a existência de uma correlação entre a linha de "números" e a linha de "expoentes". O número 40, por exemplo, está entre os números 10 e 100. Se o expoente 1 gera o número 10 e o expoente 2 gera o número 100, existe um expoente entre 1 e 2 que irá gerar o número 40. Para provar esta suposição, Napier fez mais alguns cálculos, o que resultou na tabela 2.
Nesta nova tabela foi possível perceber que o número 40 está entre os números 39,81 e 50,11. Estes, por sua vez, são gerados pelos expoentes 1,6 e 1,7. A correlação ainda se mantinha e notou que se criasse uma nova tabela com valores de exponenciais de 1,60 até 1,70 se aproximaria ainda mais do número 40. Napier fez isso mais algumas vezes. Ao final destas observações ele escreveu:
Logarithmorum 40
basis 10 aequalis 1,602059...
Cuja tradução do latim é:
A evolução do número 40 na base 10 é igual a 1,602059...
E que se aprende na escola como é mostrado na equação 2.
Iog10 40 = 1,602059...
Sim, para John Napier, um número evoluiu de uma escala (números reais) para outra escala (logarítmica). Isso significa dizer, matematicamente, o que é mostrado na equação 3.
10 1,602059 = 40
Isto é válido para qualquer base. Veja o exemplo dado na tabela 3, com a base 2, para obter a evolução (logaritmo) do número 40.
O número 40 está entre os números 32 e 64, que são gerados pelos expoentes 5 e 6. Fazendo uma nova escala de expoentes de 5,0 até 6,0 tem-se a tabela 4.
Agora o número 40 está entre os números 39,39 e 42,22. Estes são gerados pelos expoentes 5,3 e 5,4. Extrapolando essa ideia, Napier escreveria:
Logarithmorum 40 basis 2
aequalis 5,321928...
Cuja tradução do latim é:
A evolução do número 40 na base 2 é igual a 5,321928...
A notação da escola é a da equação 4.
log2 = 5,321928
Seu contraponto exponencial é mostrado na equação 05.
25,321928 = 40
Qual a importância disto?
Ao ler o artigo até aqui, você leitor, deve estar se perguntando: e daí? Para que serve esta mudança para uma escala logarítmica, esta tal "evolução" de um número?
Aqui está a grande, e genial, descoberta de John Napier: perceber que mudar um número para uma escala logarítmica permite que as operações matemáticas sejam mudadas também, simplificando os cálculos. Calma, eu explico. Se você pensar em termos exponenciais vai compreender algumas propriedades interessantes. Pense na multiplicação de números gerados por exponenciações, como na equação 6.
22 x 24 = 22 + 4 = 26 = 64
Se ao invés de escrever uma base e seu expoente, fossem utilizados os números que resultam destes cálculos, teriam o mesmo resultado, fornecido na equação 7:
4 x 16 = 64
Napier reparou que a propriedade de soma exponencial também se aplica a evolução dos números, ou seja, aos logaritmos. Onde antes era necessário fazer uma multiplicação, passou-se a fazer apenas uma adição, operação matemática muito mais simples de executar, como mostra a equação 8.
log2(4) + log2(16) = log2(4 x 16) = 2 + 4 = 6
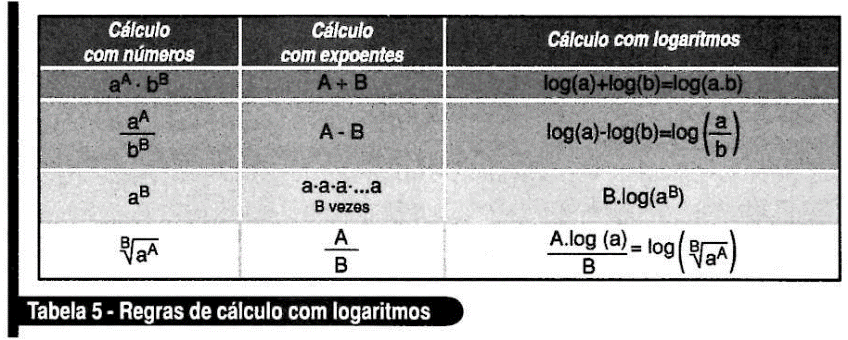
Essa característica foi testada para todas as outras operações, e se chegou à conclusão mostrada na tabela 5.
Um cálculo de multiplicação com números transforma-se em soma com logaritmos. Um cálculo de divisão vira subtração. A potenciação passa a ser multiplicação e a radiciação será feita através de divisão.
Em uma época em que as máquinas de cálculo ainda não haviam sido inventadas, isto reduziu (e muito) o tempo necessário para resolver complicadas equações.
f(x) = loga(x)
Aplicações em Eletrônica
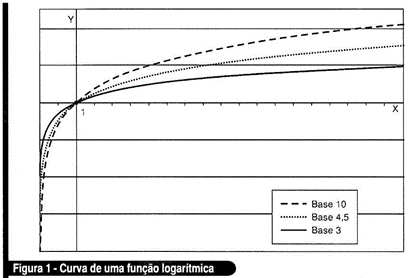
Não importa qual é a base utilizada: sempre uma função logarítmica (equação 9) tem uma curva com a característica mostrada na figura 1, que mostra uma propriedade interessante: não importa qual é a base. a curva sempre passará pelo ponto (x = 1, y = 0).
Diversos componentes na eletrônica têm comportamento logarítmico, como é o caso da carga de capacitores, da reatância indutiva, etc. O som também é percebido por nossos ouvidos através de uma escala logarítmica. Assim, alguns controles de volume, feito através de potenciômetros, devem ter escala logarítmica.
No próximo artigo abordaremos uma importante aplicação dos logaritmos: o decibel (dB). Até lá.
*Alessandro F. Cunha é engenheiro elétrico, trabalha em Telecomunicações desde 1994 e é professor da rede SENAI.