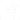Em muitos circuitos eletrônicos, principalmente nas aplicações em telecomunicações, nos deparamos diante de diversos modos de ligações de filtros de frequência. Às vezes são necessárias várias ligações em série, paralelo, ou mesmo ligações mistas, entre diferentes filtros, para se obter uma determinada curva de resposta de frequência.
Nota: Artigo publicado na Revista Saber Eletrônica de março de 1983.
A simples análise de apenas olhar as ligações entre os filtros, muitas vezes, nos confunde, dependendo da maneira em que os filtros se interligam. Isto me levou a encontrar um método para determinar a curva de resposta de frequência através de conjuntos.
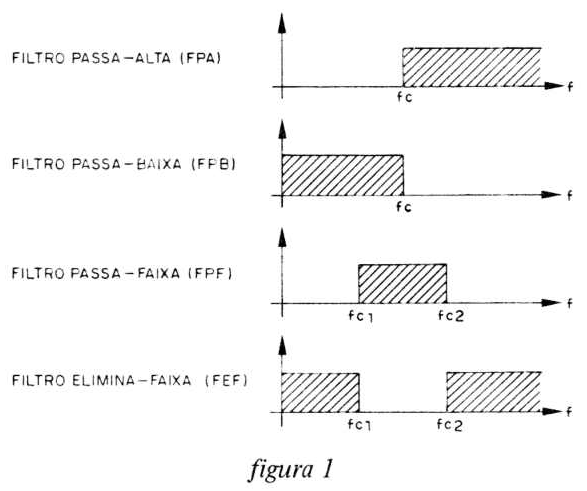
Primeiro recordaremos os quatro tipos de filtros utilizados e suas respectivas respostas de frequência na figura 1.
Vamos agora supor que desejamos encontrar a curva de resposta de frequência da seguinte ligação dos filtros K(FPA), L(FPB) e M(FPF). (figura 2)
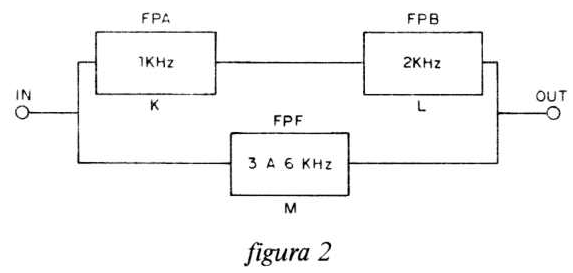
O primeiro passo é representar cada filtro por um conjunto de elementos. Os elementos por suas vezes devem representar as faixas de frequência que passam pelos filtros.
Como cada filtro representa um conjunto, temos o conjunto K, conjunto L e o conjunto M. O filtro K é o filtro passa-altas (1 KHz), seu conjunto é, portanto, formado pelas faixas de frequência acima de 1 KHz. O filtro L é um filtro passa-baixas e é formado por todas as faixas de frequência abaixo de 1 KHz; e o filtro M somente pela faixa de frequência de 3 a 6 KHz por ser um filtro passa-faixas.
Como as faixas de frequência são os elementos dos conjuntos, temos:
de 0 a 1 KHz - chamaremos de elemento A
de 1 a 2 KHz - elemento B
de 2 a 3 KHz - elemento C
de 3 a 6 KHz - elemento D
de 6 KHz a 00 - elemento E
A figura 3 nos mostra os filtros representados pelos conjuntos e seus respectivos elementos.
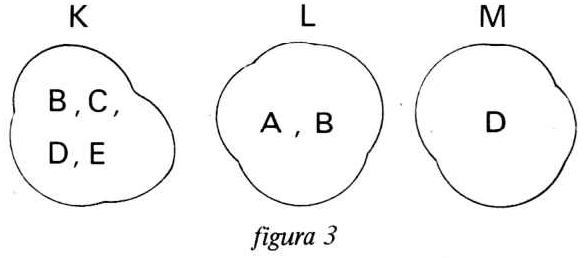
Passamos então para a solução do circuito, como se fosse um circuito resistivo, ou seja, primeiro resolve-se os filtros K e L que estão em série e o resultado dos dois em paralelo com o filtro M.
Para filtros em série faremos a interseção de seus conjuntos e para filtros em paralelo a união dos mesmos.
Como K e L estão em série, façamos a interseção, ou seja, formamos um conjunto dos elementos que estão contidos tanto em K como em L. (figura 4)
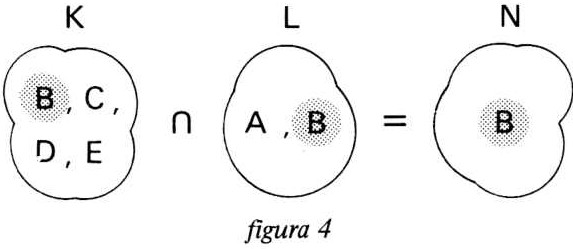
O conjunto resultante denominaremos de conjunto N, que representa um filtro passa-faixas de 1 a 2 KHz (elemento B), que resultou da associação em série dos filtros K e L. (figura 5)
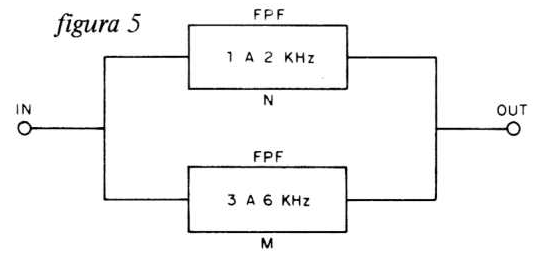
Como o filtro resultante está em paralelo com o filtro M, então a união deles é o que temos na figura 6.
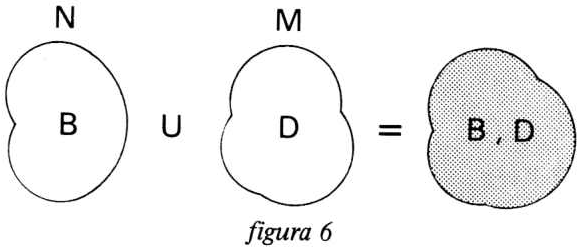
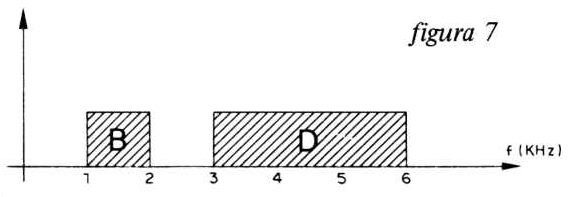
O filtro equivalente total da associação contém os elementos B e D, que representam as faixas de frequência que passam pelo filtro, 1 a 2 KHz e 3 a 6 KHz que é um filtro passa-faixas. A curva de resposta pode ser facilmente produzida, já que o filtro "deixa passar" as faixas B e D de frequência. (figura 7)
Resolveremos agora um outro circuito, incluindo um filtro elimina-faixa (figura 8).
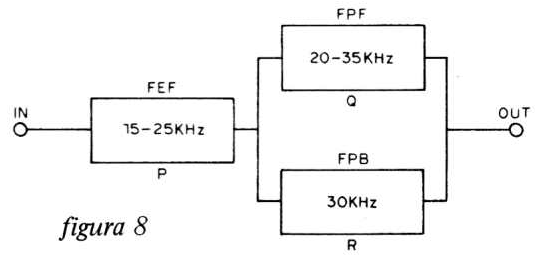
Note que todas as frequências envolvidas no circuito formarão as faixas de frequência, ou seja: para o filtro elimina-faixa temos 15 KHz e 25 KHz, para o filtro passa-faixas temos 20 KHz e 35 KHz e para o filtro passa-baixas 30 KHz, que ordenados formam os elementos dos conjuntos:
de 0 a 15 KHz = A
de 15 a 20 KHz = B
de 20 a 25 KHz = C
de 25 a 30 KHz = D
de 30 a 35 KHz = E
de 35 KHz a ꝏ= F
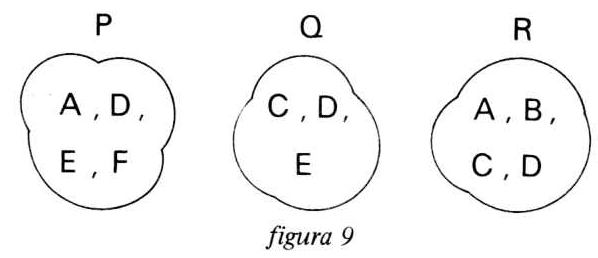
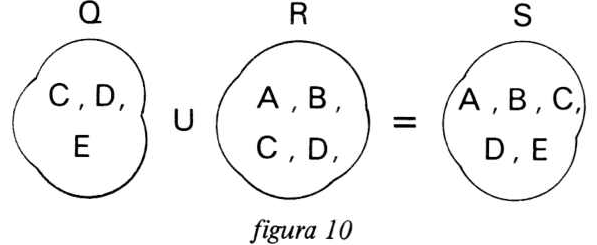
Para o filtro P, por ser elimina-faixa, seus elementos de conjunto são A, D, E, F. Os elementos são sempre as faixas de frequência que passam pelo filtro. A figura 9 mostra os conjuntos e seus respectivos elementos referentes aos filtros da figura 8. Como Q eR estão em paralelo, a união deles fica como mostra a figura 10.
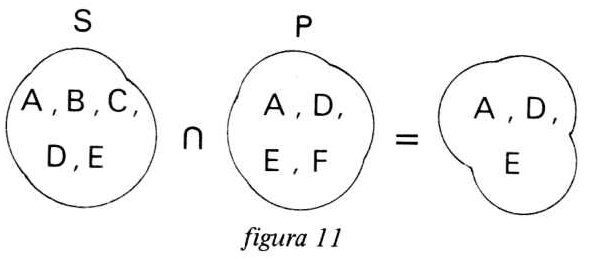
O conjunto resultante S representa um filtro em série com P, portanto, a interseção Sn P é o que mostra a figura 11.
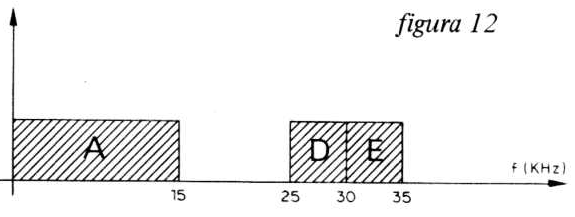
O conjunto resultante de todo o circuito, representa um filtro de frequência equivalente ao circuito da figura 8, cujas faixas de frequência A, D e E são as faixas de frequência que passam pelo circuito. A resposta de frequência fica, portanto, como mostra a figura 12.