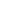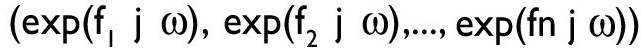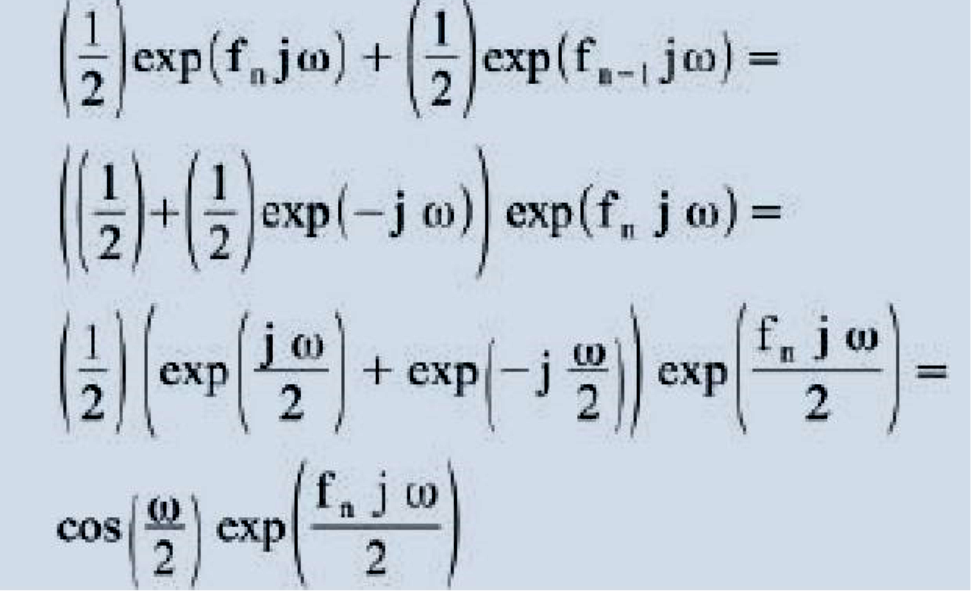Este artigo abordará duas das técnicas em Processamento Digital de Sinais. Uma delas é a tradicional DFT - Discrete Fourier Transform, ou Transformada Discreta de Fourier, e a outra é a utilização de uma alternativa chamada de Transformada Wavelet.
Nota: Artigo publicado na Revista Saber Eletrônica 466 de dezembro de 2012
Pretende-se mostrar aqui quais são as situações onde cada uma das técnicas é propícia (ou não) e em quais casos, bem como abordar de maneira geral cada uma delas, mostrando uma pequena introdução conceitual, um código-fonte em linguagem C++ para o cômputo da DFT e exemplos práticos do uso das técnicas de Fourier e Wavelets no reconhecimento de sinais neurofisiológicos e também na compressão de imagens utilizadas pelo FBI americano.
Não se pode mais imaginar o mundo sem o Processamento Digital de Sinais (ou DSP) — Digital Signa! Processing - como é comumente chamado. Em linhas gerais, ele está presente nas mais diversas aplicações, tais como:
• Controlando o volume e a tonalidade de som no processador do seu CD-player;
• Reconhecendo padrões na área de visão por computador;
• Na área de instrumentação eletrônica médica, identificando características em sinais neurofisiológicos, tais como eletrocardiograma (ECG) e eletroencefalograma (EEG), entre outros;
• No controle automático industrial.
A principal vantagem do Processamento Digital de Sinais é realizar por intermédio de algoritmos computacionais, o que antes se fazia somente por intermédio de circuitos eletrônicos. Para isso, várias "ferramentas" foram ganhando espaço e vários algoritmos foram sendo adaptados. Dentre as principais, podemos citar a Transformada de Fourier e a Transformada Wavelet.
A Transformada de Fourier já é um instrumento bastante difundido, enquanto que a Transformada Wavelet ainda é um assunto obscuro para a maioria dos leitores. Ambas as técnicas são largamente empregadas na pesquisa científica atualmente, sendo que essa última, em alguns casos, propicia a obtenção de informações não conseguidas com o uso da DFT.
Muitos tipos de sinais podem ser melhor analisados no domínio da frequência ao invés de no domínio do tempo, ou seja, estudando quais frequências existem no sinal ao invés de qual é a amplitude do sinal em cada instante de tempo. Se, por exemplo, dentro de um período de tempo de 0,5 segundo, temos um sinal cossenoidal que contém 4 frequências: 10, 25, 50 e 100 Hz, a sua representação gráfica no domínio do tempo fica conforme mostra a figura 1.
No eixo horizontal está o tempo e no vertical está a amplitude do sinal. Em contraparte, a representação desse sinal no domínio da frequência está exibida na figura 2, onde no eixo horizontal está a frequência e no vertical está a sua amplitude.
Essa representação do sinal no domínio da frequência nos permite ter uma ideia de qual (ou quais) frequência(s) está(ão) presente(s) no sinal. Note na figura 2, que quando a frequência é igual a 10, 25, 50 ou 100 Hz, a amplitude é muito alta, pois essas são as frequências existentes no sinal, enquanto que para os outros valores de frequência, sua amplitude é praticamente nula. A Transformada Discreta de Fourier, concebida pelo matemático francês Jean Baptiste Fourier, é a técnica que permite, a partir de um sinal no domínio do tempo, obter o sinal correspondente no domínio da frequência. Matematicamente, ela é definida como:
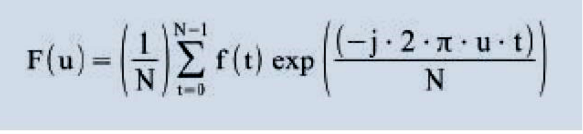
É possível também realizar a operação inversa, ou seja, a partir do sinal no domínio da frequência, obtermos um representação no domínio do tempo. Para isso, basta utilizarmos a Transformada Discreta de Fourier Inversa, definida como:

Nas equações acima, u é a frequência, N é o número de amostras do sinal, t é o instante de tempo e j é o número complexo √-1.
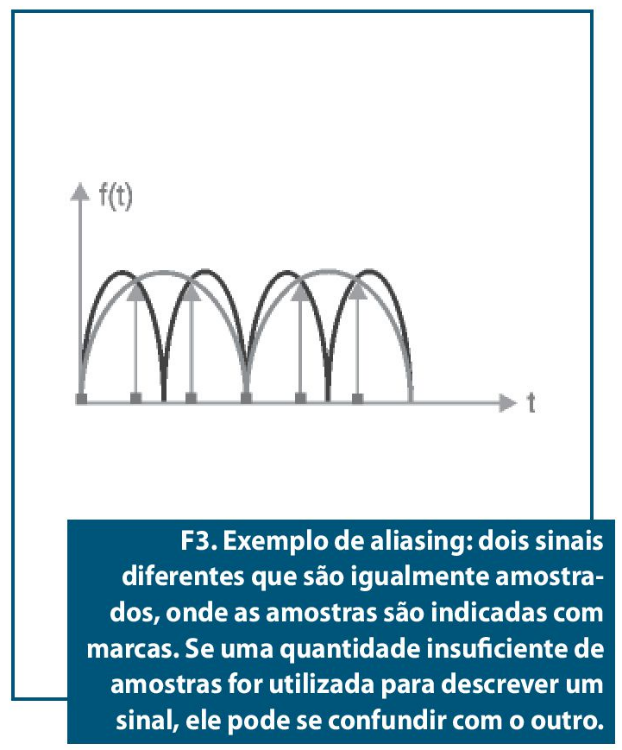
É importante salientar que o termo "discreta" implica em que não usamos todos os infinitos valores da função no domínio do tempo para obtermos a representação no domínio da frequência, e vice-versa. Ao invés disso, discretizamos o sinal, ou seja, tomamos amostras igualmente espaçadas ao longo do sinal. De acordo com o famoso Teorema de Nyquist, a quantidade de amostras necessárias para descrevermos perfeitamente o sinal deverá ser pelo menos o dobro de sua frequência máxima. Se menos amostras forem utilizadas, o sinal não poderá ser perfeitamente descrito, devido a um efeito conhecido como aliasing. A figura 3 exemplifica o fato.
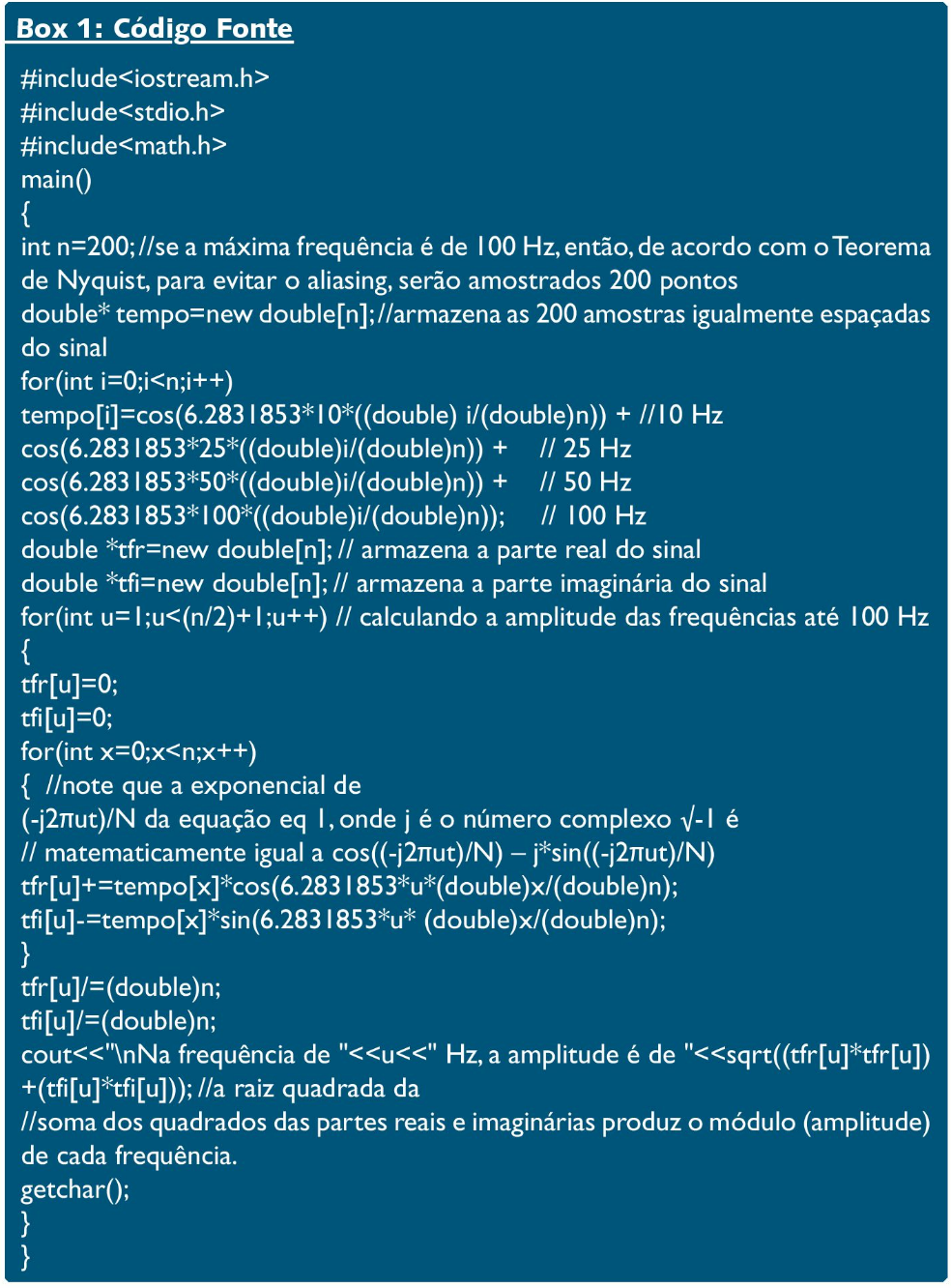
O código-fonte, escrito em linguagem C++ (box 1), permite realizar o cômputo de uma DFT de um sinal do cossenoidal que contém as quatro frequências do exemplo anterior. O programa realiza os cálculos e exibe na tela as amplitudes do sinal nas frequências de até 100 Hz, mostrando a forte presença das 4 frequências em questão.
Para podermos tratar agora da classe de Transformadas Wavelets, se faz necessário apresentarmos duas definições:
• Definição I: Um sinal é dito estacionários, quando possui sempre a mesma frequência (ou frequências) ao longo de todo o período de tempo para o qual é definido.
• Definição 2:A energia de um sinal é definida pela soma dos quadrados dos valores de suas amplitudes no domínio do tempo.
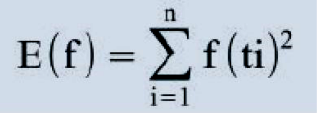
Transformada Wavelet
A DFT diz exatamente qual é (ou quais são) a(s) frequência(s) presente(s) num sinal. Se estivermos analisando um sinal estacionário, ou seja, um sinal que tem frequência constante, sabemos que a frequência apontada como existente pela DFT está presente em todo o sinal. Mas, se estivermos trabalhando com um sinal não estacionário, muito embora a DFT aponte as frequências presentes, ela não diz nada sobre a localização dessas frequências, ou seja, em que instante de tempo determinada(s) frequência(s) aparece(m). Quando essa informação é importante, a DFT não serve e então, devemos lançar mão de outra técnica. Uma delas é usar uma decomposição baseada em Wavelets.
A tradução literal de Wavelet é ondaleta, ou pequena onda. Embora possa parecer um termo estranho, o leitor se familiarizará com ele à medida que aprofundar seus estudos nesse campo. As principais aplicações práticas para o uso de Wavelets são:
• Detecção de características em sinais (imagens, sons e outros sinais)
• Compressão de imagens e sons
• Filtragem de ruído em imagens e sons
• Identificação de características em sinais.
A Transformada Discreta Wavelet decompõe um sinal em outros dois sinais, fazendo uso de filtros passa-baixas (chamados scaling signals) e filtros passa-altas (chamados wavelets signals).
Para um sinal discreto F de n pontos, existem m (m <= n/2) scaling signals (V1, V2, ..., Vm) e m wavelets signals (W1, W2, ....,Wm). Cada par de vetores formados pelo conjunto (V1, W1), (V2, W2) …, (Vm, Wm) é ortogonal, ou seja, possuem produto escalar igual a 0. A forma como se define essa base de vetores é que dá origem a diferentes classes de Transformadas Wavelets, que se prestam melhor a uma ou outra determinada situação, entretanto, independentemente dessa definição, os scaling signals serão sempre filtros passa-baixas e os wavelets signals serão sempre filtros passa-altas.
Quando m = (n/2), o vetor de n pontos formado pelos coeficientes (ai, a2, am), seguido de (dl, d2, ..., dm), é chamado de Transformada Wavelet nível I do sinal original. Este processo de decomposição é conhecido como Análise de Multi-Resolução (MRA - MultiResolution Analysis) e é o coração da análise de sinais com Wavelets.
Como exemplo, mostramos abaixo a Transformada de Haar - nível I, que é o tipo mais simples de Transformada Wavelet. Para ela, os vetores V1, Vm e W1 ..., Wm são definidos como sendo:

Supondo que o sinal discreto F seja: F = (f1,f2,f3,f4,f5,f6,f7,f8) = (4,6, 10,12,8,6,5,5) (é o sinal original que possui n = 8 pontos). Sua Transformada de Haar - nível 1 será: H = (a1 ,a2,a3,a4,d1 ,d2,d3,d4), sendo que:
Daí: H = (5√2, I I √2, 7√2, 5√2, - √2, - √2, √2, 0). O processo descrito trata-se, na verdade, de uma combinação linear do sinal original com cada scaling signal e com cada wavelet signal. É possível também encontrarmos H de uma outra maneira, adotando uma outra técnica de cálculo para os coeficientes (a1,a2,a3,a4,d1 ,d2,d3,d4):

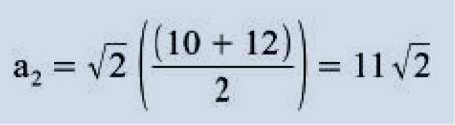
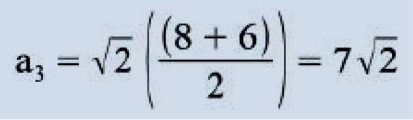
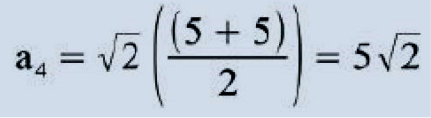


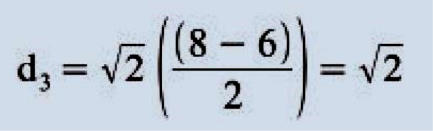
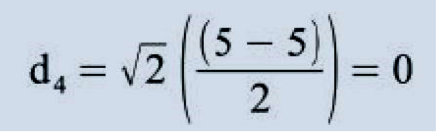
Daí: H = (5√2, I I √2, 7√2, 5√2, - √2, - √2, √2,0). Note bem que nessa segunda técnica, fundamentalmente, para obter cada um dos (n/2) primeiros pontos de H, fazemos uma média de cada par de pontos de F, e para obter cada um dos (n/2) últimos pontos de H, fazemos uma diferença de cada par de pontos de F, sendo que essa segunda técnica é equivalente à primeira. Os valores obtidos através dessas médias e diferenças são multiplicados por √2 apenas para efetuar um pequeno ajuste (com o intuito de conservar a energia do sinal, conforme será explicado adiante) levando assim ao mesmo resultado da primeira técnica.
A razão para termos dado essa segunda técnica de cálculo de H é a de mostrar que as médias e diferenças citadas provocam no sinal F, o efeito da aplicação de filtros passa-baixas e passa-altas respectivamente, como veremos a seguir.
Antes de prosseguir, fica interessante verificar uma propriedade importante: de acordo com a definição de energia dada acima, a energia do sinal original F é:4² + 6² + 10²+ 12² + 8² + 6² + 5² + 5² = 446 e a energia da Transformada de Haar - nível 1 do sinal é: (5√2)² + ( I I √2)² + (7√2)² + (5√2)² + (-√)² + (-√2)² + (√)² +(0)²= 446 do mesmo modo. Em diversas aplicações, essa propriedade será de fundamental importância.
Filtragem Passa-baixa: Média das Amostras Vizinhas
Para descobrir a resposta em frequência de um filtro, trocaremos cada amostra de um sinal discreto F no domínio do tempo (f1, f2, …, fn) por sua representação em frequência. Sendo assim, F passa a ter os componentes
, onde j é o número complexo √-1 e W (lê-se ômega) é a frequência angular do sinal. Se cada componente do sinal de saída do filtro é a média entre dois componentes vizinhos do sinal original, então, a resposta em frequência de cada um desses componentes será:
Nesse caso, I cos(ɯ/2) I é a resposta em frequência de cada componente do novo sinal. Para todo sinal discreto não costumamos medir a frequência em hertz, mas sim em radianos. Sendo assim, π é a máxima frequência do nosso sinal em questão. Substituindo w por π, cos(π/2) tende a 0. Substituindo por 0 (frequência 0 = corrente contínua), cos(0/2) resulta em 1, ou seja, não haverá alteração no sinal original. Se, quando a frequência é baixa (próxima a 0) quase não existe variação no sinal e quando é alta (próxima a π) o sinal é quase que todo atenuado, temos um filtro passa-baixa.
Filtragem Passa-alta: Diferença das Amostras Vizinhas
Similar ao que foi feito no caso anterior, vamos fazer agora a diferença das metades das amplitudes dos sinais:
Nesse caso, I sin(w/2) I é a resposta em frequência de cada componente do novo sinal. Substituindo w por π, sin(p/2) tende a 1. Substituindo por 0 (frequência 0 = corrente contínua), sin(0/2) resulta em 0. Se, quando a frequência é baixa (próxima a 0) quase todo o sinal é atenuado e quando é alta (próxima a π) o sinal quase não sofre alteração, temos um filtro passa-alta.
Separação de Componentes de Diferentes Frequências do Sinal e Análise MRA de Múltiplos Níveis
Quando obtemos a Transformada Wavelet de um sinal discreto, estamos realizando a Transformação nível 1. Se calcularmos a Transformada Wavelet da primeira metade desse sinal já transformado, estaremos no segundo nível de análise, e assim por diante.
Este processo, que está exibido na figura 4, pode se repetir por log2(n), onde n é o número de pontos do sinal original. A Transformação nível 1 é composta pelos sub sinais A e B, a Transformação nível 2 é composta pelos sub sinais C, D e B e a Transformação nível 3 pelos sub sinais E, F, D e B. No nosso sinal F dos exemplos anteriores, podemos ir até o nível 3 de MRA, já que ele é definido por 8 pontos discretos.

Exemplos de Aplicação
Mostramos a seguir algumas aplicações práticas do uso das técnicas de Processamento Digital de Sinais mencionadas.
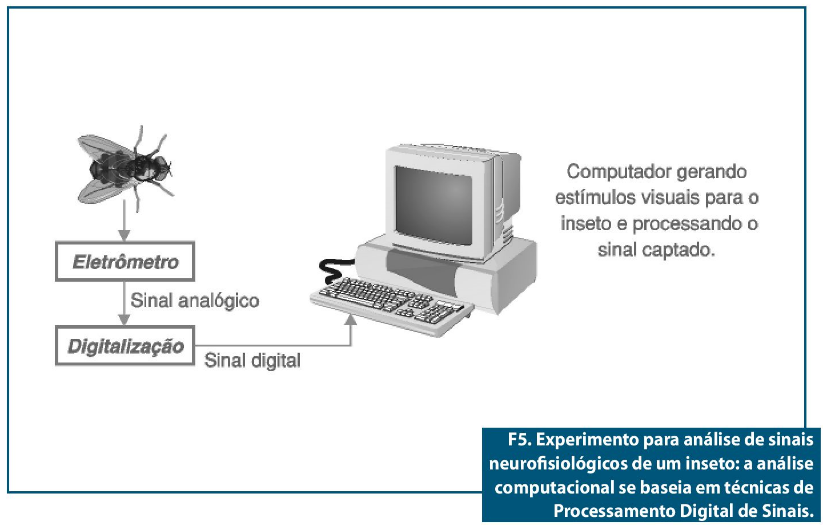
O sistema descrito na figura 5 trata de uma aplicação na área de sinais médicos / neurofisiológicos. Tem por função, estudar a reação dos neurônios responsáveis pelos estímulos visuais de um inseto, que representa um modelo simplificado para o cérebro humano. O experimento é composto pelas seguintes partes e equipamentos:
• Um suporte de aprisionamento do inseto, com um eletrodo espetado na região dos neurônios (para isso, se faz necessário um potente microscópio).
• Um eletrômetro (multímetro muito sensível) e um circuito para captar os sinais, que são analógicos.
• Um sistema para digitalização dos sinais para serem analisados pelos algoritmos computacionais.
• Um computador para processar os algoritmos e também para gerar estímulos visuais para o inseto. As reações provocadas pelos neurônios, quando estes percebem os estímulos gerados pelo monitor, geram o sinal captado pelo eletrômetro e o circuito associado.
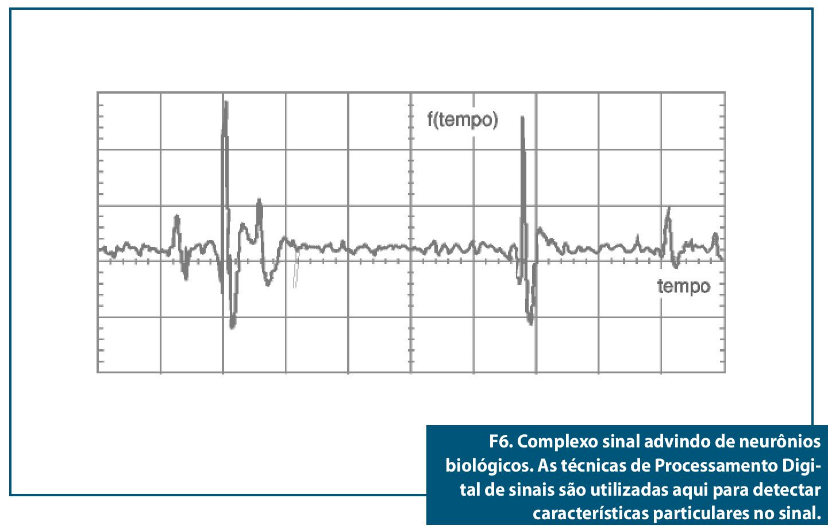
A análise computacional do sinal acima permite decifrar, em um sinal do tipo mostrado na figura 6, as particulares reações elétricas geradas por determinados neurônios.
Um outro exemplo interessante, ilustrado na figura 7, é o de compressão de dados. A parte da esquerda mostra uma imagem monocromática original no formato BMP. A parte da direita, mostra a mesma imagem, que ocupa cerca de 10 vezes menos espaço para armazenamento. Esta compressão, adotada pelo FBI americano, é realizada da seguinte forma:
• Calcula-se a Transformada Wavelet da imagem.
• Desprezam-se os componentes de alta frequência que não interessam e estão abaixo de um determinado "limiar".
• Calcula-se a Transformada Wavelet Inversa da Imagem, obtendo a nova imagem.

Estes exemplos, no entanto, não representam nada frente à quantidade de aplicações existentes. A Internet possui muito material interessante sobre o assunto, especialmente em www.wavelets.org.
Conclusão
As Transformadas Wavelet consistem numa classe de funções de diversidade imensa. Após a leitura do presente artigo, deverá ter ficado claro para o leitor que a DFT de um sinal apenas traz a informação de qual(is) frequência(s) existe(m) no sinal, mas não informa onde elas se localizam, no caso de um sinal não estacionário.
Como o assunto é vastíssimo, o presente texto serve apenas como uma referência introdutória, sendo que outras informações podem ser obtidas nas bibliografias indicadas ou na Internet.