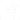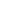A Agilent Technologies (www.agilent.com) em seu Application Note 1588 descreve a maneira de se escolher um osciloscópio em função de sua largura de faixa para uma determinada aplicação. Na análise de sinais de altas frequências, esta característica é fundamental para que se possa visualizar de maneira precisa uma forma de onda. Neste artigo damos o conteúdo principal deste application note que pode ser baixado na, versão original em inglês a partir do site da Agilent
Nota: Artigo publicado na Revista Saber Eletrônica 436 de maio de 2009.
O osciloscópio é um dos instrumentos mais importantes na bancada de trabalhos de todo profissional da eletrônica. Com as aplicações em telecomunicações alcançando cada vez frequências mais elevadas, a seleção de um osciloscópio apropriado torna-se urna tarefa crítica quando se pretende equipar um laboratório. Mais do que isso, mesmo nos laboratórios que possuam diversos desses instrumentos disponíveis, é preciso saber em um dado momento qual deve ser eleito para uma determinada tarefa.
A Faixa Passante de um Osciloscópio
Todos os osciloscópios respondem a uma determinada faixa de frequências, que é limitada a um valor máximo dependente das características de seus circuitos. Os osciloscópios típicos para frequências até 1 GHz e abaixo liso possuem o que se denomina resposta Gaussiana, na qual ocorre uma atenuação suave, conforme mostra a figura 1.
As curvas do osciloscópio podem ser comparadas a de um filtro passa-baixas. Assim, às frequências máxima e normalmente determinada para o ponto em que a atenuação é de -3 dB a partir do nível de referência. Os osciloscópios com especificações de faixa maiores do que 1 GHz têm uma resposta de frequência plana, geralmente do tipo exibido na figura 2. Veja que o ponto de transição é mais agudo do que no caso anterior.
Existem vantagens e desvantagens para cada um dos dois tipos de osciloscópios. Aqueles que têm uma resposta plana atenuam menos os sinais na faixa menos do que os que possuem uma resposta Gaussiana. No entanto, os osciloscópios com resposta Gaussiana atenuam menos os sinais que estão fora da faixa de resposta, o que significa que eles possuem tipicamente um tempo de subida mais rápido do que um que tenha uma resposta normalmente plana.
Entretanto, existem aplicações em que é interessante atenuar os sinais que estejam fora da faixa de frequências. Isso fará com que componentes de altas frequências capazes de causar falseamentos sejam eliminados. A Agilent tem no Application Note 1587 um estudo sobre isso. De qualquer forma, é importante conhecer sempre qual é a resposta do osciloscópio, seja ela plana ou Gaussiana. A verificação da largura de faixa de um osciloscópio pode ser feita com a ajuda de um gerador de sinais senoidais que gere sinais de varredura de faixa. A atenuação no ponto de -3 dB normalmente se traduz em um erro de amplitude de 30%.
Uma outra especificação importante para os osciloscópios é o tempo de subida ou "rise time" Instrumentos com uma resposta Gaussiana têm um tempo de subida de aproximadamente 0,35/fbw, onde fbw é o limite da faixa de frequências, baseado em um critério de 10% a 90%. Já osciloscópios com resposta máxima-plana têm especificações de tempo da ordem de 0,4ifbw. Uma maneira de se testar o tempo de subida de um osciloscópio é aplicar pulsos que sejam de 3 a 5 vezes mais rápidos do que as especificações dele para esta característica.
Como uma regra geral, a largura de faixa de seu osciloscópio deve ser pelo menos 5 vezes maior do que o clock digital mais rápido do seu sistema que está sob teste. Se o osciloscópio satisfizer este critério, ele poderá capturar até o quinto harmônico de um sinal com um mínimo de atenuação. Este componente do sinal é muito importante para determinar a forma de onda final de um sinal digital, Mas se você necessita fazer medidas precisas de frontes de alta velocidade, esta fórmula não vai levar em conta as componentes de alta frequência embutidas nas subidas e descidas dos sinais rápidos. A regra geral é então:

Um método mais preciso para determinar a faixa exigida para um osciloscópio é se basear na frequência mais alta presente nos sinais digitais, que não seja a frequência máxima de clock. Esta frequência será baseada nas maiores taxas de subida e descida dos frontes dos sinais. Assim, a primeira coisa que se faz é determinar os tempos de subida e descida dos sinais mais rápidos. Estas informações podem ser obtidas diretamente das folhas de dados dos componentes utilizados.
Em primeiro passo determine as taxas mais rápidas de subida e descida dos sinais
A seguir, em um segundo passo pode-se utilizar a fórmula sugerida pelo livro "High Speed Digital Design — A Handbook of Back Magic". Estas fórmulas são:

onde:
ƒknee= frequência "de joelho"
Para sinais com características de tempo baseadas em limiares de 10%e 80%, fknee é igual a 0,5 dividido pelo tempo de subida do sinal. Para sinais com características de subida baseadas nos limiares 20% a 80%, o que é comum em alguns dispositivos modernos, a fknee é igual a 0,4 dividido pelo tempo de subida do sinal.
O terceiro passo consiste em se determinar a faixa exigida para o osciloscópio que vai medir o sinal, baseado no grau desejado de precisão para a subida e descida dos sinais. A tabela 1 apresenta vários graus de precisão para osciloscópios Gaussianos e de Resposta Plana.
Damos a seguir algumas medidas feitas em um sinal digital de clock com características como as citadas até agora no artigo, para servir de exemplo.
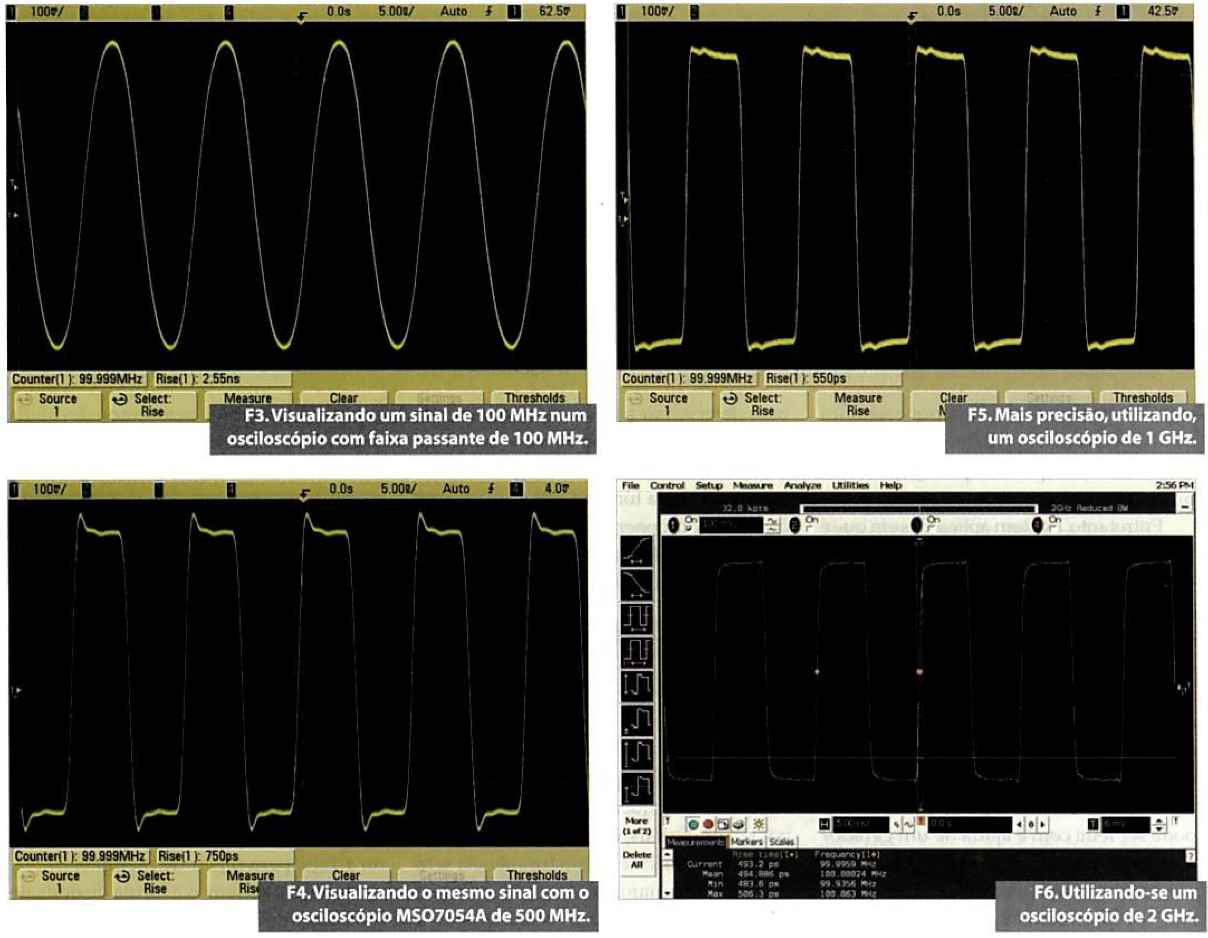
Na figura 3 temos a forma de onda de um sinal digital de clock de 100 MHz com fronte de 500 ps (10-90%) visualizada em um osciloscópio Agilent MS06014A com faixa passante de 100 MHz. Conforme pode-se observar, este osciloscópio visualiza apenas o sinal fundamental de 100 MHz, o que resulta numa imagem com forma de onda senoidal. Um osciloscópio deste tipo consiste numa solução para se trabalhar com sinais abaixo de 20 MHz, mas não para se visualizar o sinal de clock de 100 MHz.
Com a utilização do osciloscópio M507054A de 500 MHz, já temos a apresentação de uma forma de onda diferente, conforme ilustra a figura 4.
Com este osciloscópio é possível capturar o quinto harmônico do sinal, que é a primeira regra a ser seguida ao se visualizar uma forma de onda. Mas, na medida do tempo de subida, vemos que o osciloscópio mede aproximadamente 750 ps. Neste caso, o osciloscópio não está fazendo uma medida muito precisa. Ele está, neste caso, medindo alguma coisa próxima do seu próprio tempo de subida da ordem de 700 ps, não o tempo de subida do sinal de entrada, que está próximo de 500 ps.
Para medir este tempo será preciso empregar um osciloscópio com uma faixa passante ainda mais larga. Utilizando-se então um MS07104A de 1 GHz da Agilent, temos a forma de onda mostrada na figura 5.
Quando selecionado o tempo de subida, o osciloscópio mede 550 ps, o que significa uma precisão de aproximadamente 10%, que pode ser aceitável em muitos casos. No entanto, mesmo com esta faixa passante ainda existem aplicações em que se necessita de uma precisão maior. Assim, usando-se um osciloscópio de 2 GHz, como o DS08020413 da Agilent, temos a visualização da forma de onda da figura 6.
Observe que o tempo de subida apresentado por este osciloscópio é de aproximadamente 495 ps para o sinal observado, o que é uma excelente precisão.
A Agilent com sua "série Infinium" de osciloscópios oferece a possibilidade do upgrade da faixa de frequências. Assim, o profissional pode adquirir o tipo de 2 GHz e depois ir fazendo o upgrade até 13 GHz. Veja, portanto, que a ideia passada de que um osciloscópio deveria ter uma largura de faixa pelo menos 3 vezes maior do que a frequência mais elevada a ser observada, não vale mais quando tratamos de sinais digitais, RF modulada.
Conclusão
Pelas imagens do Application Note da Agilent podemos notar a diferença entre uma forma de onda real de um sinal e a forma observada em osciloscópios com diversas larguras de faixa. O modo como a largura de faixa afeta a precisão das observações é muito importante nas aplicações que exigem maior precisão. Na documentação da Agilent, que pode ser acessada no site da empresa, existem considerações adicionais que podem ser de grande interesse para os leitores que desejam saber mais sobre o assunto.