As pontes de medida consistem num recurso importante que o profissional da eletrônica conta para a determinação de diversas grandezas no laboratório ou bancada de desenvolvimento de projetos. Se bem que possamos contar com instrumentos precisos para a medida de resistências, indutâncias, capacitâncias e freqüências, existem casos em que as propriedades das pontes tornam-nas mais apropriadas para um trabalho. Neste artigo falaremos de algumas das principais pontes de medida.
A maioria dos nossos leitores conhece a ponte de Wheatstone, usada na medida de resistências e que serve de ponto de partida para muitos estudos de laboratório de instrumentação.
No entanto, para esta mesma maioria, existem muitas outras pontes que são desconhecidas, mas cuja importância não é menor do que a própria Ponte de Wheatstone.
É dessas pontes que vamos falar neste artigo.
O QUE É UMA PONTE
Uma ponte nada mais é do que um circuito de medida que faz uso de uma fonte de sinal ou de tensão contínua e um detector de nulo que pode ser um fone de ouvido, um indicador de bobina móvel ou qualquer outro conforme o tipo de aplicação exija, tudo isso conforme mostrado na figura 1.
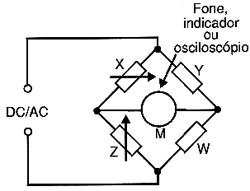
Quando os componentes desta ponte apresentam uma determinada relação de valores, não há sinal ou não circula corrente pelo detector de nulo.
Diz-se, nestas condições, que a ponte se encontra em equilíbrio.
Se tivermos um componente de valor desconhecido, e tivermos um componente variável que compense seu valor, poderemos sempre obter o equilíbrio da ponte ajustando o componente variável.
Isso significa que podemos dotar o componente variável de uma escala de tal forma que nos permita determinar o valor do componente desconhecido, quando for alcançado o equilíbrio.
Conforme os componentes usados, o tipo de grandeza que vai ser medida as pontes recebem diversas denominações que passamos agora a analisar.
PONTE DE THOMSON
Esta é uma ponte muito interessante destinada à medida de resistências muito baixas, menores que 1 ohm.
Esta ponte recebe o nome de seu descobridor que a desenvolveu em 1862, tendo o circuito básico mostrado na figura 2.
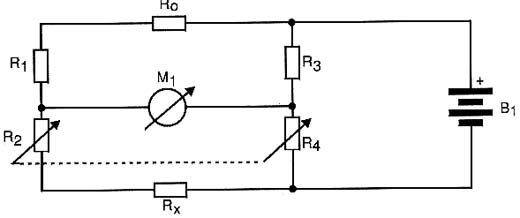
As resistências do circuito devem manter inicialmente as seguintes relações de valores:
R1 = R3
R2 = R4
A resistência Ro é fixa e tem um valor que deve ser aproximadamente o valor da resistência que se espera medir (Rx).
As resistências R2 e R4 são conjugadas, ou sejam variam ao mesmo tempo por um eixo único.
Nestas condições o nulo da ponte será obtido quando as resistências do circuito satisfizerem a seguinte igualdade:
Rx = Ro (R4/R3)
A principal vantagem no uso deste tipo de ponte é que a influência da resistência dos fios que fazem a ligação a Rx pode ser eliminada, o que é importante quando se mede resistências muito baixas.
PONTE DE SAUTY
A Ponte de Sauty tem seu circuito mostrado na figura 3 e serve para a medida de capacitâncias.
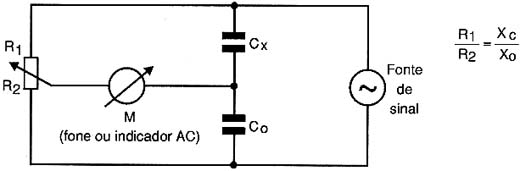
O que se faz nesta ponte é trocar um dos resistores da ponte de Wheatstone por um capacitor e além disso aplica-se na alimentação um sinal de freqüência de acordo com os capacitores a serem medidos.
Desta forma, as reatâncias capacitivas do capacitor a ser medido e de um capacitor de referência é que são usadas no equilíbrio da ponte.
Chamando-se de Xc a reatância do capacitor a ser medido e de Xo a reatância do capacitor de referência, o equilíbrio da ponte vai ser conseguido quando a seguinte relação de valores entre todos os elementos da ponte for satisfeita:
R1/R2 = Xc/Xo
Trabalhando-se com um fone de ouvido de alta impedância e com sinais na faixa de 1 kHz a 5 kHz a detecção de nulo ser feita no ponto em que o som desaparecer.
Para capacitâncias muito pequenas pode-se usar sinais de freqüências mais altas e como detector de nulo um osciloscópio.
Um problema que pode ocorrer neste tipo de ponte vem do fato de o capacitor medido pode não apresentar uma capacitância pura.
Lembramos que um capacitor real tem uma certa resistência parasita em série a ser considerada.
Um resistor variável pode ser agregado em série com o capacitor de referência também para compensar esta resistência parasita caso em que o equilíbrio, ao ser conseguido, leva tanto a determinação da capacitância Cx como a resistência parasita ligada em série, conforme mostra a figura 4.
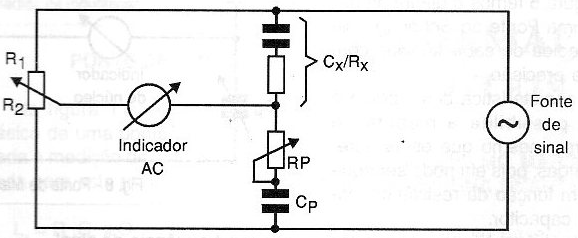
Variações da ponte de Sauty existem para medição de capacitores eletrolíticos caso em que se agregam elementos como uma fonte de polarização contínua para este componente, indutâncias e capacitâncias com a finalidade de filtrar correntes contínuas e sinais usados nos testes.
PONTE DE SCHERING
Na figura 5 temos o diagrama básico de uma Ponte de Schering que é usada na medida de capacitâncias com excelente precisão.
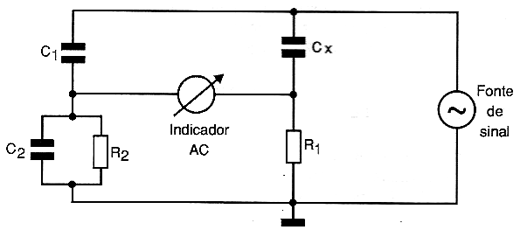
Uma característica desta ponte é que ela possibilita a medida de capacitores mesmo que apresentem fugas, pois ela pode ser equilibrada em função da resistência paralela ao capacitor.
A fonte de sinal vai depender dos valores a serem medidos, assim como o detector de nulo.
Para capacitores comuns na faixa de 1 nF a 1 uF pode-se usar um gerador de sinais de 1 kHz e um fone de ouvido como elementos da ponte.
O equilíbrio desta ponte ocorre quando as seguintes relações entre os componentes forem satisfeitas:
Cx = C1 (R1/R2)
Rx = R1 (C2/C1)
Onde Cx é a capacitância do capacitor em teste e Rx a resistência de fuga.
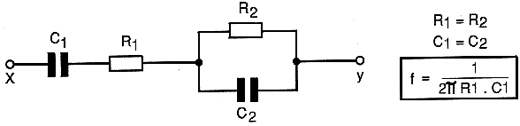
PONTE DE WIEN
Uma característica importante das pontes que vimos até agora é que seu equilíbrio independe da freqüência do sinal de entrada.
Para a medida de sinais de áudio, uma ponte interessante, que na verdade foi a que deu origem à ponte de Schering, é a chamada ponte de Wien, mostrada na figura 6.
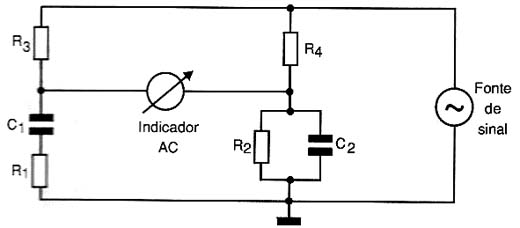
Esta ponte equilibra-se quando um capacitor Cx adquire um valor tal que:
Cx = 1/(R1.R2.C1.?)
Onde: ? = 2 . p. f, sendo f a freqüência do sinal
Se o capacitor utilizado é variável, previamente ajustado em função dos demais elementos pode-se determinar a freqüência do sinal.
Fazendo-se com que:
R3 = 2.R4
C1 = C2
O equilíbrio da ponte ser obtido quando:
f = 1/(2.p.Cx.R2)
Veja o leitor que esta configuração é a mesma utilizada nos denominados osciladores por ponte de Wien, cujo circuito básica do elo de realimentação que determina a freqüência é mostrada na figura 7.
PONTE DE MAXWELL
Esta ponte, cujo diagrama básico é mostrado na figura 8, é utilizada na medida de indutâncias.
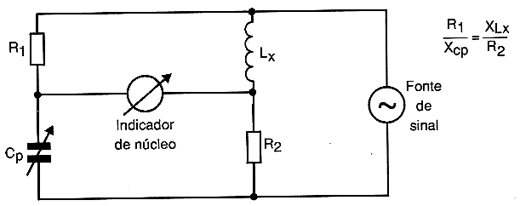
A idéia básica é fazer a comparação de uma indutância com uma capacitância, com base em suas reatâncias, isso porque é mais difícil obter-se um padrão de indutâncias do que de capacitâncias.
Assim, quando esta ponte está em equilíbrio temos a relação mostrada no próprio diagrama.
O equilíbrio ocorre quando as reatâncias, da bobina e do capacitor de referência, adquirem valores que mantém uma proporção que depende dos valores dos resistores dos outros braços.
A freqüência do sinal usado vai depender da ordem de grandeza da indutância que se pretende medir.
Um aperfeiçoamento desta ponte é mostrado na figura 9 em que se acrescenta ao circuito também um resistor variável.
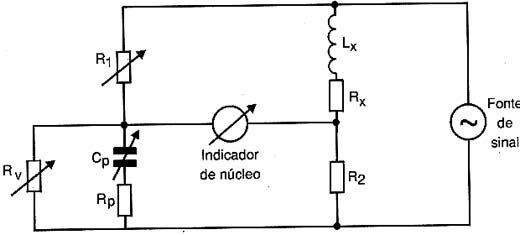
Este componente é necessário para se equilibrar a ponte levando-se em conta também a resistência ohmica do enrolamento da bobina que se soma à sua indutância.
Lembramos que a bobina equivale, em seu circuito real, a uma indutância ligada em séria com uma resistência.
Veja que o equilíbrio desta ponte é feito por meio de dois ajustes e um ponto importante é que, através da medição tanto da indutância, como da resistência associada, pode-se ter uma idéia também de seu fator de qualidade (fator Q).
PONTE DE HAY
Esta ponte, cujo diagrama básico é mostrado na figura 10, também se destina à medida de indutâncias.
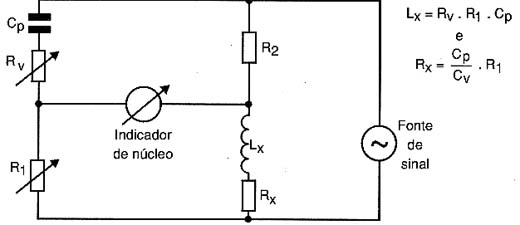
O princípio de funcionamento é o mesmo da ponte de Maxwell, utilizando-se um capacitor para equilibrar com sua reatância, a reatância apresentada por um indutor, que está sendo medido.
O equilíbrio desta ponte vai ser conseguido quando a relação de valores de componentes mostrada em seu diagrama for alcançada.
PONTE DE OWEN
Na figura 11 temos o diagrama básico de uma ponte de Owen que é destinado a medição de indutâncias.
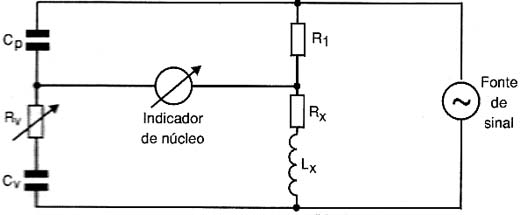
Esta ponte tem por característica importante o fato de seu funcionamento não depender da freqüência do sinal.
No diagrama temos a relação de valores de componentes que deve ser satisfeita para que ela fique em equilíbrio.
CONCLUSÃO
As pontes são de grande importância nos laboratórios de medidas eletrônicas.
Neste artigo demos uma pequena noção sobre seus tipos e utilidades.
No entanto, os circuitos indicados, quando levados à equipamentos profissionais podem ter recursos adicionais importantes como por exemplo controles de sensibilidade, seleção de faixas de valores medidos, além de detectores de nulo com diversos níveis de sensibilidade e outros.