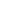Um dos recursos mais importantes na manutenção, reparação e ajuste de equipamentos eletrônicos é a visualização das grandezas que variam com o tempo em seus circuitos através um osciloscópio. Para o caso específico da medida de frequências, amplitudes e fases com a ajuda desse instrumento, é fundamental conhecer as figuras de Lissajous. Mais do que isso, elas também podem ser usadas com outras finalidades, inclusive na geração de efeitos em editores de imagens para a Internet e recursos multimídia. Neste artigo mostramos o que são as figuras de Lissajous, como podem ser geradas, para que servem e ainda como interpretar suas formas utilizando-as como poderosa ferramenta de diagnóstico eletrônico.
A maioria dos sinais elétricos com que trabalhamos possui uma forma de onda senoidal, conforme mostra a figura 1. 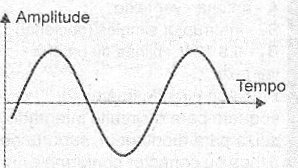
Figura 1 – Sinal com forma de onda senoidal.
Esta forma indica o modo como uma tensão ou uma corrente varia com o tempo. Esta figura é, portanto, traçada colocando-se em sequência pontos cujas posições no eixo vertical depende da intensidade do sinal num instante que têm sua correspondência no eixo horizontal. Qual é a origem desta forma de onda? O que realmente significa sinal ter uma forma de onda senoidal ?
A SENÓIDE
Imaginemos um ponto P que gira com velocidade uniforme segundo uma trajetória perfeitamente circular, conforme ilustra a figura 2.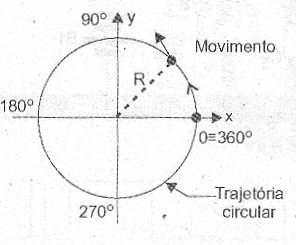
Figura 2 – O movimento circular uniforme (MCU).
Partindo do ponto O podemos medir (ou indicar) a posição desse ponto por meio de um ângulo, que é formado pela linha que o liga ao centro do círculo (sua trajetória) e pelo eixo de referência X, de acordo com a figura 3.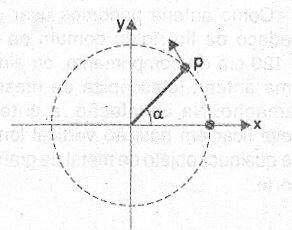
Figura 3 – A posição de um ponto P que realiza um movimento circular.
Vemos então que a ¼ de uma volta completa corresponde um ângulo de 90o e que a uma volta inteira corresponde um ângulo de 360o. A indicação da posição do ponto em cada instante pode ser feita com o valor de um ângulo, em graus. Mas, essa não é a única forma de indicar a posição do ponto no movimento que ele realiza. Levando em conta que o comprimento de uma circunferência é numericamente igual a duas vezes o seu raio multiplicado pelo fator PI (p), podemos medi-la em "radianos", ou seja, em frações ou múltiplos de seu próprio raio.
Como a volta inteira corresponde a 2p radianos, podemos facilmente estabelecer relações desta grandeza com outros ângulos, conforme se observa na seguinte tabela:
90 graus = π/2 radianos
180 graus = π radianos
270 graus = 3π/2 radianos
360 graus = 2 π radianos
As duas unidades para a medida de ângulos ou da posição de um ponto numa circunferência são usadas em Eletrônica e outras ciências como a Matemática e a Física. Para nós é importante seguir com o nosso ponto em movimento e analisar o que ainda poderá ocorrer.
Em cada instante do seu movimento podemos agora fazer uma projeção sobre o eixo Y (vertical) de modo a medir sua "altura" em relação ao eixo X. Essa distância, mostrada na figura 4, pode assumir valores positivos e negativos quando o ponto realiza uma volta completa na circunferência.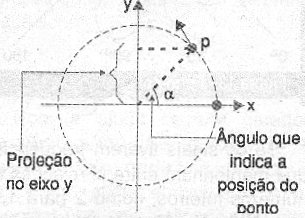
Figura 4 – A projeção de P no eixo Y.
Se considerarmos o valor do raio da circunferência unitário (igual a 1), essa distância (que depende do ângulo que determina a posição do ponto) variará de –1 a +1 e a ela podemos associar uma grandeza denominada "seno" do ângulo, ou abreviadamente "sen". Se em toda a volta do ponto anotarmos os senos dos ângulos correspondentes a um bom número de posições e os colocaremos um ao lado do outro, obteremos uma figura ondulada, conforme ilustra a figura 5.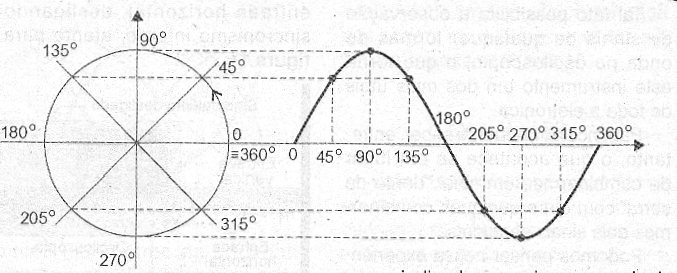
Figura 5 – Desenvolvendo uma senoide.
Esta figura é chamada de "senoide" e nada mais é do que uma representação gráfica da projeção do movimento do ponto na circunferência sobre o eixo vertical ou eixo Y. Passemos agora a um mundo que mais nos interessa, que é o da Eletrônica. Vamos imaginar uma espira que corte o campo magnético de um ímã em forma de ferradura, tal como num gerador, o que é apresentado na figura 6.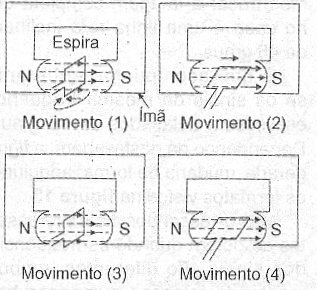
Figura 6 – Gerando uma tensão senoidal.
Partindo da posição 1, a espira se move inicialmente no campo paralelamente às suas linhas de modo que, neste instante. a tensão gerada é nula. Uma fração de segundo depois, a espira já começa a curvar sua trajetória de modo a cortar as linhas do campo segundo ângulos que vão aumentando até que em 2 ela já o faz perpendicularmente, quando a indução é máxima. A partir do ponto 2 a trajetória continua se curvando, agora no sentido de que o ângulo entre seu movimento e as linhas de força vai diminuindo até que em 3 ela volta a cortar as linhas paralelamente. Neste trecho (de 2 a 3) a tensão diminui.
Após o ponto 3, novamente o ângulo segundo o qual a espira corta as linhas vai aumentando, mas agora no sentido contrário ao que ocorria anteriormente. A tensão induzida vai aumentando, mas com polaridade oposta ao trecho inicial. Temos então a indução de uma tensão negativa que atinge seu máximo em 4. A partir do ponto 4 a tensão negativa se reduzirá até zero de modo a voltarmos à situação inicial como em 1.Na volta completa da espira teremos então a indução de um ciclo de uma tensão alternada, cuja forma de onda representada na mesma figura é senoidal.
É importante observar que a variação da tensão representada tem uma forma muito bem definida, que não deve ser confundida com duas "meias circunferências" conforme mostra a figura 7 e que nada tem a ver com a senóide.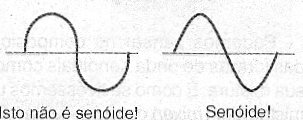
Figura 7 – A verdadeira senoide.
Muitos circuitos oscilantes como, por exemplo, os de duplo T, LC e de deslocamento de fase podem gerar correntes que variam da mesma forma que a indicada, ou seja, geram sinais senoidais. Os osciloscópios são instrumentos que permitem visualizar a forma de onda de um sinal que seja aplicado na sua entrada vertical, veja a figura 8.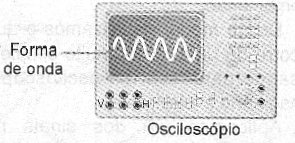
Figura 8 – Observando um sinal senoidal no osciloscópio.
Um sinal interno de sincronismo cuja forma de variação é denominada "dente de serra" combina-se com o sinal que deve ser observado, e o resultado é visto na figura 9.
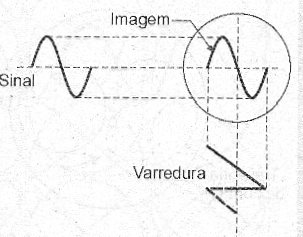
Figura 9 – Combinando sinais para visualização.
Observe que o sinal "dente de serra" quando combinado com qualquer outro tipo de sinal, resulta numa imagem que corresponde a este último tipo de sinal. Tal fato possibilita a observação de sinais de quaisquer formas de onda no osciloscópio, o que torna este instrumento um dos mais úteis de toda a eletrônica. Para nós é importante saber, entretanto, o que acontece se em lugar de combinarmos um sinal "dente de serra" com outro qualquer, combinarmos dois sinais senoidais. Podemos pensar nessa experiência não apenas considerando o uso de sinais elétricos, mas também de qualquer fenômeno que varie segundo um padrão senoidal como, por exemplo, a oscilação de pêndulos, dois movimentos circulares que se combinem, ondas sonoras, etc.
Vamos partir em nosso exemplo tomando duas circunferências que giram uma sobre a outra, observe a figura 10. É justamente a composição de sinais senoidais como a que ocorre neste caso, que nos leva à formação das denominadas Figuras de Lissajous.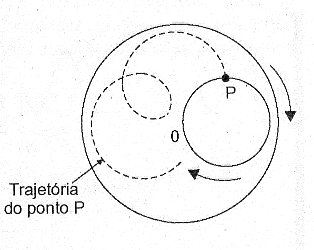
Figura 10 – Circunferências girando uma sobre a outra.
AS FIGURAS DE LISSAJOUS
Podemos pensar na composição das formas de onda senoidais como a sua mistura. É como se tivéssemos um misturador (mixer) capaz de juntar dois sinais de características diferentes, obtendo-se um efeito final que é a sua combinação. Desse modo, visualizamos o que ocorre de uma forma muito simples, usando para isso um osciloscópio imaginário inicialmente. Aplicamos um dos sinais na entrada vertical e o outro sinal na entrada horizontal, desligando o sincronismo interno, conforme ilustra a figura 11.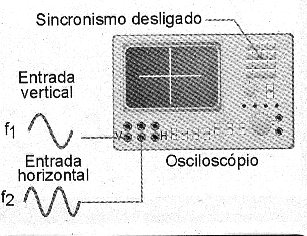
Figura 11 – Aplicando sinais nas duas entradas com o sincronismo interno desligado.
Vamos partir inicialmente de dois sinais de mesma frequência e mesma fase, como mostrado na figura 12, em que analisaremos a formação da figura resultante, ponto a ponto.
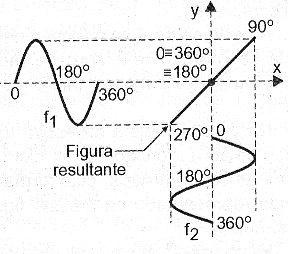
Figura 12 – Combinando sinais de mesma frequência e fase.
Tomamos em cada instante o ponto correspondente à intensidade de um sinal e também do outro, traçando linhas de projeção que se cruzarão determinando assim o local do espaço em que irá aparecer o ponto correspondente da imagem que será gerada. Numerando estes pontos podemos traçar a imagem completa que no caso é uma linha reta inclinada de 45 graus. O que aconteceria, entretanto, se os sinais de mesma frequência estivessem defasados de 45 graus? Dependendo da desfasagem, a figura gerada mudaria de forma, adquirindo os formatos vistos na figura 13.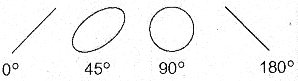
Figura 13 – Figuras para sinais de mesma frequências, porém com fases diferentes.
Mas os desenhos mais interessantes se obtêm quando as frequências dos sinais são diferentes, embora mantendo relações numéricas bem determinadas. Se os sinais tiverem frequências que mantenham entre si relações de números inteiros, como 2 para 1, 3 para 2, 5 para 4, etc. as figuras que serão formadas adquirem aspectos bastante interessantes.
Na figura 14 temos um exemplo de figura formada quando os sinais possuem uma relação de frequência de 2 para 1, sendo que o sinal aplicado na varredura horizontal é aquele que tem a frequência mais alta.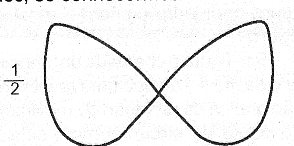
Figura 14 – Figura para sinais com relação de frequência de 2 para 1.
O mais importante disso é que através da simples observação de uma figura formada por dois sinais, poderemos descobrir muito de um deles, se conhecermos o outro.
Para Saber Mais
Os leitores que tiverem dificuldades em entender a "matemática" de nossas explicações ou que desejarem ir além calculando o que deverá resultar da combinação de senoides de determinadas frequências podem procurar nos livros de Física informações no capítulo que trata de "Composição de MHS ou Movimentos Harmônicos Simples".
USANDO AS FIGURAS DE LISSAJOUS PARA MEDIDAS DE SINAIS
Existem duas formas de trabalhar com as Figuras de Lissajous para se medir amplitude, frequência e fase de sinais senoidais. Veja que é preciso ter os recursos para se visualizar essas figuras. O mais comum é o osciloscópio, mas elas podem ser produzidas em computadores e mesmo por sistemas mecânicos.
a) Sinal único
Com a ajuda de um gerador de sinais senoidais ligado a uma das entradas, podemos descobrir as características de qualquer sinal senoidal que seja aplicado na outra entrada. Este fato torna as figuras de Lissajous um importante recurso para o diagnóstico de problemas em equipamentos, ou ainda para a medida de frequências sem que para isso seja necessário usar um frequencímetro. Para medir a frequência de um sinal empregando as figuras de Lissajous o que precisamos fazer inicialmente é aplicar o sinal desconhecido numa das entradas do osciloscópio, por exemplo a vertical. Na horizontal, vamos ligar um gerador de sinais senoidais e ajustá-lo até que tenhamos uma figura estável em que possamos contar os lóbos ou protuberâncias formadas.
Vamos supor que, conforme mostra a figura 15, a figura formada tenha 3 lóbos na parte horizontal e dois na vertical.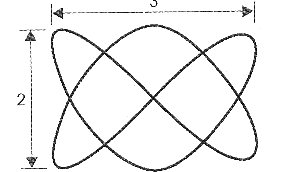
Figura 15 – Figura gerada com 3 lóbos horizontais e 2 verticais.
Sabemos que a relação de frequências para os sinais aplicados é de 3 para 2. Dessa forma, se a frequência do sinal aplicado na varredura horizontal que serve como referência for de 1500 Hz, por exemplo, a frequência do sinal desconhecido será de 1000 Hz. Veja, então, que o maior cuidado que o operador que está realizando as medidas deve ter é ir ajustando vagarosamente seu gerador de sinais para que possa encontrar uma posição em que a figura tenha poucos lóbos tanto na horizontal como na vertical, e assim fique fácil contá-los. Uma relação de frequências de 235 para 234, por exemplo, não apenas tornaria praticamente impossível a contagem dos lóbos mas também não poderia ser obtida com a devida estabilidade. Na figura 16 temos diversas figuras que são formadas para relações de frequências mais comuns.
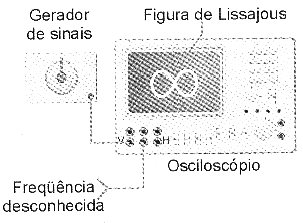
Figura 16 – Usando o osciloscópio e Figuras de Lissajous para medir frequências.
No caso específico dos sinais de mesma frequência quando obtemos retas, elípses ou circulos nas figuras, podemos medir também a defasagem do sinal, o que é outro recurso importante deste tipo de análise.
b) Dois sinais
Neste caso, podemos usar as figuras de Lissajous para medir a fase entre eles. Basta aplicar os sinais nas entradas vertical e horizontal do osciloscópio (que terá o sincronismo interno desligado) e analisar a figura formada, que poderá ser qualquer uma das que são mostradas na figura 17.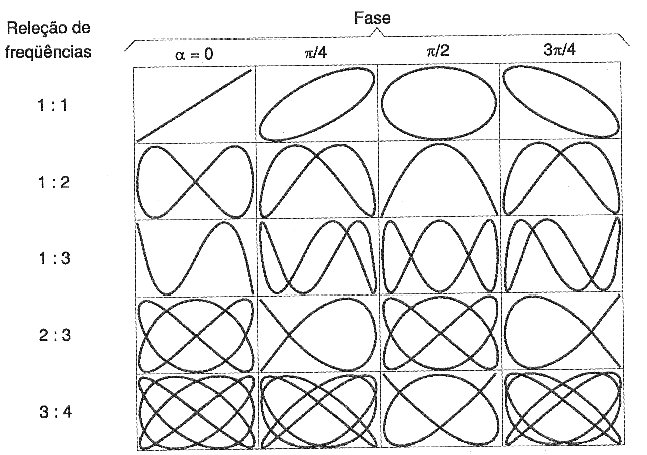
Figura 17 – Figuras para diversas relações comuns de frequências.
No computador:
Os leitores com habilidades de programação poderão escrever programas simples que gerem as figuras no monitor de seu computador. Estes programas podem ser interessantes tanto para o leitor aprender mais como para aulas quanto práticas, mostrando como serão as figuras resultantes da aplicação de frequências determinadas.
Conclusão
Temos salientado em nossos artigos a importância do osciloscópio como instrumento de bancada. Não só para visualizar as formas de onda e medir amplitudes, ele também tem outras utilidades como as que descrevemos neste artigo. O leitor que possui um osciloscópio deve familiarizar-se com as Figuras de Lissajous e seu uso e, mais do que isso, deve praticar com seu uso. Na indústria, onde problemas de defasagens de sinais da rede de energia são importantes para se determinar o fator de potência, por exemplo, o uso das Figuras de Lissajous se mostra em especial de grande utilidade, eliminando assim a necessidade de outros equipamentos.
Aplicações Recreativas
Aplicando um sistema oscilatório mecânico que movimenta um emissor de Laser ou então dois espelhos colocados em ângulo reto, é possível fazer com que o Laser se movimente segundo trajetórias que gerem as figuras de Lissajous. Com isso, é possível projetar em anteparos essas figuras criando efeitos especiais em espetáculos de todos os tipos.