Este método apresentado é muito antigo, porém simples e barato, oferecendo uma precisão muito boa, acima de um minuto e meio do grau.
Eneber C. Carvalhas
Nota: Artigo publicado na Revista Saber Eletronica 221 de 1991.
Para os leitores que possuem conhecimentos de Astronomia de Posição, este método nada difere do método das “observações duplas das alturas do sol", quando é usado o teodolito, aparelho topográfico que exige experiência em seu manuseio.
O tipo de observação usado dispensa a determinação do ângulo diastemométrico do disco solar, para a correção angular na determinação da latitude. Como a finalidade principal deste trabalho é poder usar de forma mais simples e precisa, os ótimos artigos do Professor Newton C. Braga, publicados na revista 'SABER ELETRÔNICA' n° 216 e 217, no posicionamento das antenas parabólicas, os resultados finais obtidos, sem o rigor astronômico, oferecerão resultados satisfatórios.
MONTAGEM
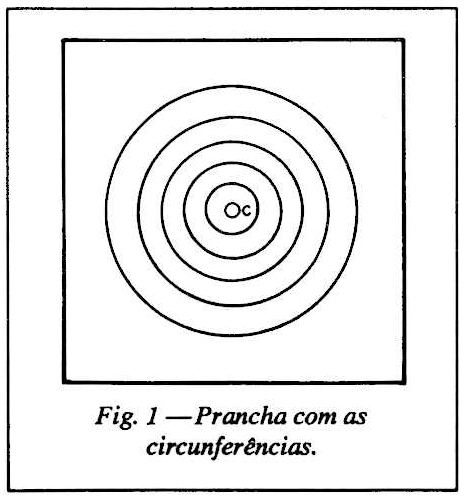
1 - Com uma prancha de madeira, medindo no mínimo 700 x 700 mm, tendo uma face preparada com tinta fosca de preferência na cor azul claro, trace pelo menos cinco circunferências concêntricas, com traço fino, firme e bastante vivo, usando como raio maior 330 mm e com separação de 66 mm para as cinco circunferências concêntricas. (Pode traçar maior número de circunferências se desejar). Escolha um lugar com boa insolação, no intervalo de 8 horas da manhã até 4 horas da tarde. Instale prancha bem fixa e nivelada. No centro desta, no ponto “c” fig. 1, instale um estilete, com o diâmetro máximo de 3 mm. Tomar o cuidado de deixar a prancha bem fixa e rigorosamente nivelada, como também o estilete rigorosamente na vertical.
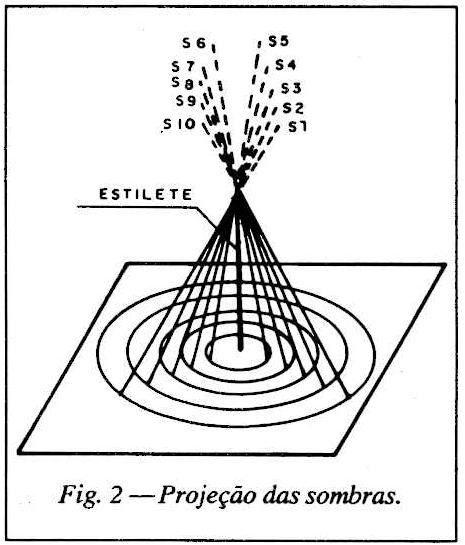
2 - Fixada a prancha conforme o descrito, estando o Sol limpo sem nenhuma nuvem no céu, vá observando a trajetória da ponta da sombra do estilete sobre a prancha. Quando a ponta da sombra tocar a primeira circunferência, marca-se um ponto neste local com um lápis. Continuando a observar a trajetória da sombra, vá marcando sobre todas as circunferências os novos pontos surgidos. Ver a fig. 2. Consultando o relógio, faltando 40 minutos para o meio-dia, vá marcando o extremo da sombra a cada 5 minutos ou tempo menor, como de 3 em 3 minutos. Esta marcação deverá ter uma simetria de tempo, isto é, começando a marcar faltando 40 minutos para meio-dia, continuar marcando até 40 minutos depois do meio-dia.
Como a sombra na parte da tarde irá aumentando, todas as circunferências marcadas na parte da manhã deverão ser marcadas na parte da tarde, isto se alguma nuvem não prejudicar a claridade do Sol. Marcada toda a trajetória da sombra, retira o estilete tomando o cuidado de medir o seu comprimento, descontando a parte que penetrou dentro da prancha. (Medidas em milímetros).
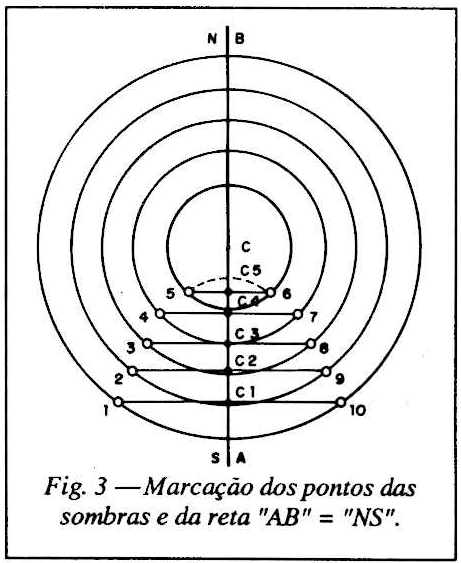
3 - Ligue todos os pontos conforme mostra a fig. 3. Corda 1 -10; corda 2-9; corda 3-8; corda 4-7; corda 5-6 e finalmente reforce os pontos de marcação simétrica, realçando a curva parabólica. Divida todas as cordas ao meio obtendo os pontos c1, c2…até c5. Ligando todos estes pontos centrais das cordas por uma reta AB, fica assim determinado o meridiano do lugar.
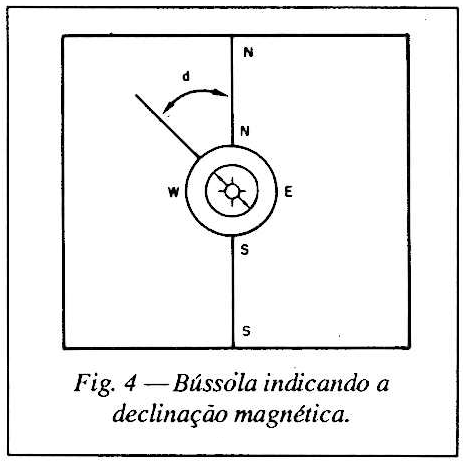
4 - Sobre esta reta AB, coloca-se uma bússola, cuja deflexão "d", mostrada na fig. 4 é a declinação magnética local, devendo anotar o seu valor como também a data (dia, mês e ano), pois a declinação magnética varia com o tempo.
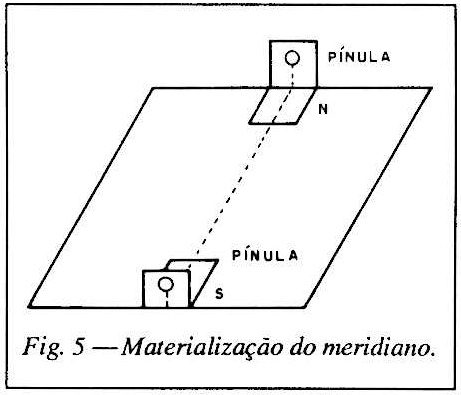
5 - Para deixar materializado o meridiano local, poderá usar o recurso mostrado na fig. 5, que consiste em duas pínulas metálicas com furos que servem de pontaria na materialização dos pontos, isto será de grande valia para futuras orientações, após a retirada da prancha.
6 - A fig. 6 nos mostra em detalhes o comprimento do estilete igual a 'h"; o afastamento %c' da sombra do estilete, que deverá ser medido em milímetros. Chamando esta medida de "s", o triângulo “bcp” nos permite calcular:
tga = h/s
Arco tangente = ang.a
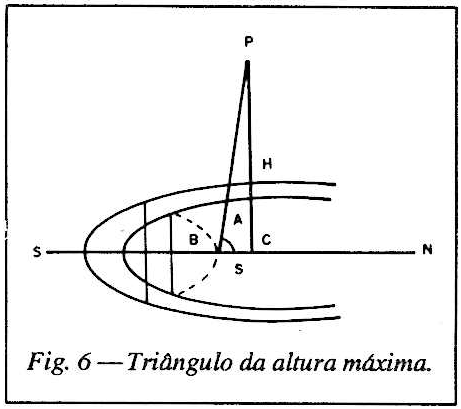
O ângulo "a' é a altura máxima do Sol sobre o meridiano do lugar. Para o cálculo da longitude podemos nos servir de qualquer mapa rodoviário, ou melhor ainda, de um mapa Nacional, mas que contenha as coordenadas marcadas em graus.
Para ilustrar como exemplo calculemos a longitude da cidade de Barretos-SP.
Usando um mapa rodoviário, Barretos está situado entre 48 graus e 49 graus de longitude oeste.
Medindo a distância entre as linhas 48 e 49 obtém-se 66 mm; do ponto que assinala a cidade de Barretos até a linha 48 tem 37mm.
Faz-se a seguinte proporção:
1 grau = 60 segs que corresponde a 66 mm temos:
66 - 60
37 - X
onde X = (37 x 60)/66 = 33,64 minutos
Longitude de Barretos-SP = 48 graus e 33,7 minutos oeste com erro menor do que um minuto do grau. Boa precisão.
Para calcular a latitude local, tem o ângulo “a" da fig. 6, e algumas considerações muito importantes a serem feitas. Primeiro é a faixa loxodrômica que é limitada no hemisfério boreal pelo trópico de câncer e no hemisfério austral pelo trópico de Capricórnio.
No dia 21 de junho o Sol acha-se no solstício de verão, ou seja, no ponto mais setentrional de sua 'carreira" que é no trópico de Câncer.
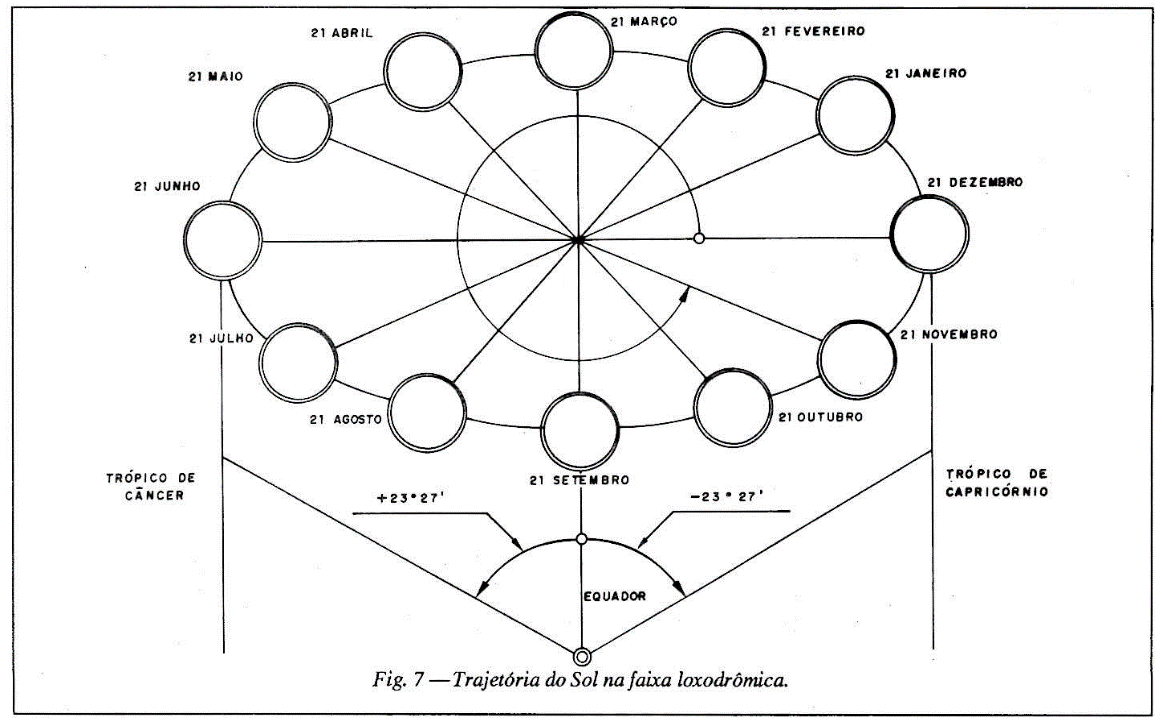
No dia 21 de dezembro, encontra-se no solstício de inverno, ponto mais meridional e que é o trópico de Capricórnio. Em 184 dias o Sol oscila numa faixa angular de 23 graus e 27 minutos para o Norte e 23 graus e 27 minutos para o Sul, conforme mostra figura 7, não sendo uniforme esta variação.
Ainda examinando a fig. 7, pode estabelecer o sentido de oscilação descrito a seguir, tomando-o contrário ao movimento dos ponteiros do relógio.
Sentido da oscilação:
• Em 21 de junho a declinação do Sol é +23 g. e 27 m.
• Em 21 de setembro a declinação do Sol é 0 g.
• Em 21 de dezembro a declinação do Sol é -23 g. e 27 m.
• Em 21 de março a declinação do Sol é 0 g.
• Em 21 de junho a declinação do Sol é +23 g. e 27 m.
Como já foi dito, a variação do Sol dentro da faixa loxodrômica não é regular.
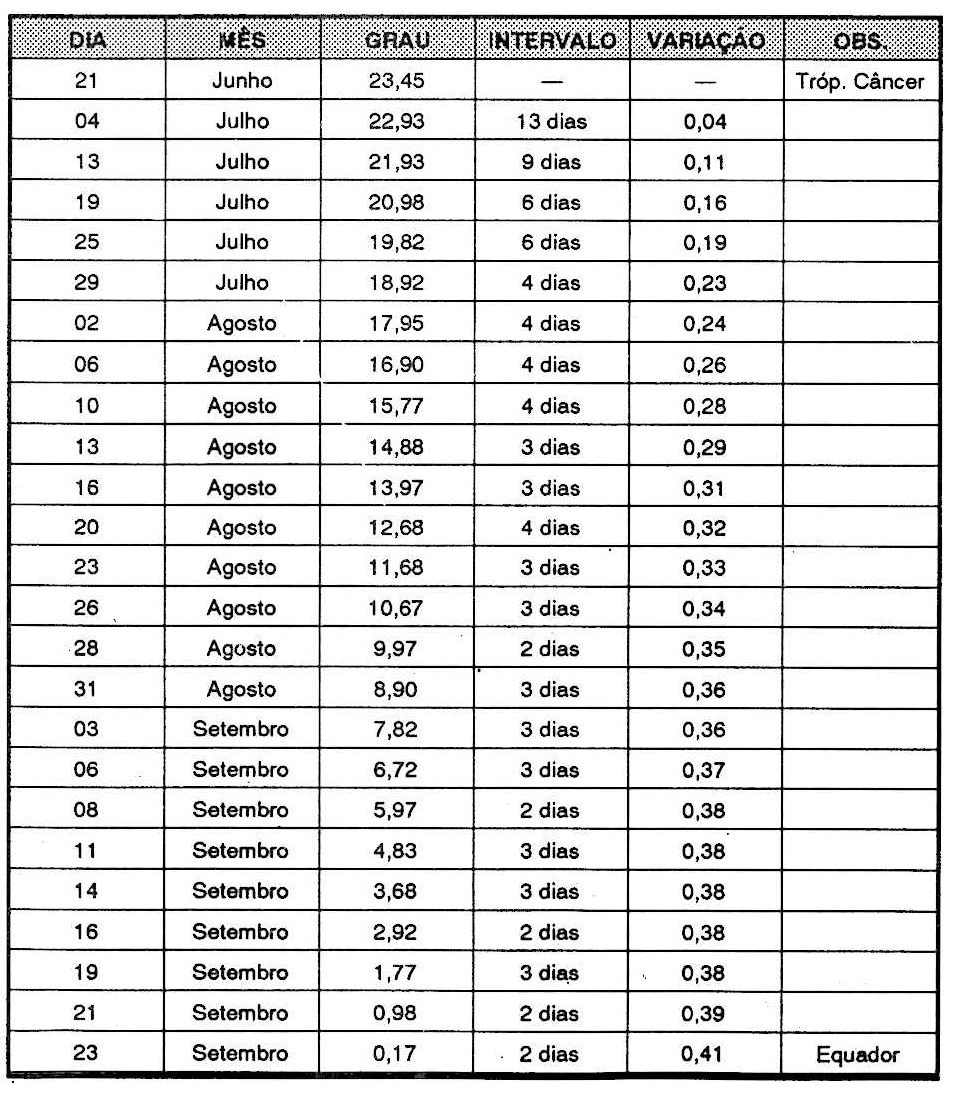
A tabela I (Variação da declinação do Sol), apresenta a variação angular partindo do trópico de Câncer até o Equador, fazendo notar a diferença dos intervalos e as variações diárias. Todos os valores angulares estão em graus decimais, e é mostrada na página seguinte.
Como exemplo ilustrativo calculemos a variação no dia 24 de fevereiro. Examinando fig. 7 conclui-se que o Sol ainda não chegou no Equador. Contando os dias decorridos entre 21 de dezembro até 24 de fevereiro, encontra-se 66 dias devendo sornar mais um dia da variação, considerando que o dia Astronômico começa no meio dia (12 horas).
Solução:
Somando os intervalos da Coluna 4 da Tabela I até o valor 68, que corresponde ao dia 28 de agosto com 9,77 graus e subtraindo 0.35 tem 9.62 graus que é o valor procurado para a declinação.
CÁLCULO APROXIMADO DA LATITUDE
Medindo a sombra do Sol no dia 24 de fevereiro, conforme a fig. 6 temos:
h = 335 mm
s= 63 mm; tg a = 335/63 = 5.3175
Arco tang a = 79,3494 graus.
Distância zenital = 90-79,3494 = 10,6506 graus.
Declinação em 24 de fevereiro... 9,6200 (Tab. I,F.7)
Latitude (Distância zenital + Declinação na data) = 20,2706 graus.
Transformando para base sexagesimal = 20 graus 16 min.
(Para facilitar os cálculos convém representar os valores dos ângulos em graus e fração decimal do grau).
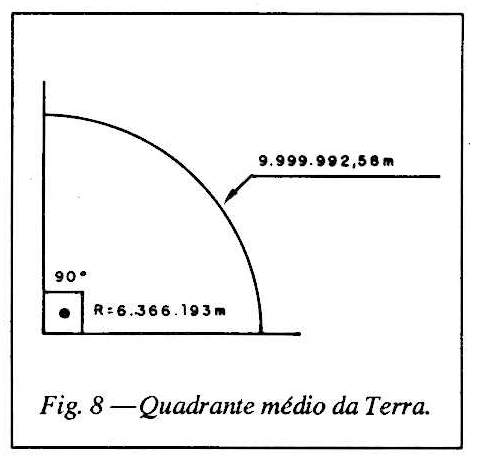
Antes de efetuarmos os cálculos finais, recordemos alguns valores importantes. O raio médio da Terra mede 6.366.193 metros. Para os cálculos geodésicos considera a Terra como uma esfera.
Portanto o comprimento de um quadrante da Terra mede 9.999.992,58 metros, num arco com 90 graus.
O comprimento de um arco de um grau é 111.111,03 metros, ver Fig. 8. Na revista SABER ELETRÔNICA n° 217, pág. 48, fig. 1, estão indicados dois satélites, um sobre o Equador Celeste e o outro no paralelo 45 graus sul. Ainda na mesma revista, consultando a Tab. I, pag 49, encontramos os satélites Brasilsat I e Brasilsat II, respectivamente 65 graus oeste e 70 graus oeste.
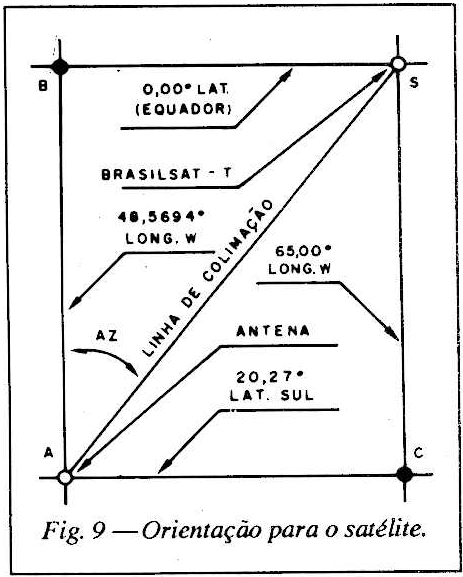
Examinando a Fig. 9 e efetuando os cálculos, obtém a diferença angular de longitude igual a 16,4306 graus e a diferença angular de latitude igual a 20,27 graus.
Para o comprimento de BS tem 16,4306 x 111.111,03 = 1.825.620,87 metros.
Para o comprimento de AB tem 20,27 x 111.111,03 = 2.252.220,58 metros. Para ter o ângulo azimutal AZ, ainda na Fig. 9, calcula-se o arco tangente BS/AB = 1.825.620,87/2.252.220,58 0,8106 cujo arco tangente = 39,0278 graus que corresponde a 39 graus 01 minuto e 40 segundos.
Para marcar a altura do satélite, o método prático descrito na revista SABER ELETRÔNICA n° 217 fig. 11, é o mais indicado, devendo partir como valor inicial do grau a altura do satélite, conforme os cálculos encontrados neste método, porém não esquecendo que a proximidade do satélite é muito grande comparada com as grandezas Astronômicas, isto é, a distância da Terra até o satélite é muito pequena.
De posse dos valores da Latitude e Longitude, como também do ângulo azimutal, faz-se uma “varredura" vertical, obtendo-se assim o sinal do satélite procurado sem variar o azimute.