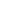1.1- Analógico e digital
Por que digital? Esta é certamente a primeira pergunta que qualquer leitor que está "chegando agora", e tem apenas alguma base teórica da Eletrônica, principalmente da eletrônica analógica, como a ensinada nos primeiros volumes desta série, faria ao encontrar o nosso curso.
Por este motivo, começamos nosso curso justamente por explicar as diferenças entre as duas eletrônicas, de modo que elas fiquem bem claras. Devemos lembrar que em muitos equipamentos, mesmo classificados como analógicos ou digitais, encontraremos os dois tipos de circuitos. É o caso dos computadores, processadores, equipamentos de telecomunicações, automatismos e instrumentos de laboratório, e muitos outros que, mesmo sendo classificados como "máquinas estritamente digitais", podem ter em alguns pontos de seus circuitos configurações analógicas.
Uma definição encontrada nos livros especializados atribui o nome “Eletrônica Digital” aos circuitos que operam com quantidades que só podem ser incrementadas ou decrementadas em passos finitos.
Um exemplo disso é dado pelos circuitos que operam com impulsos. Só podemos ter números inteiros de pulsos sendo trabalhados em qualquer momento em qualquer ponto do circuito. Em nenhum lugar encontramos "meio pulso" ou "um quarto de pulso".
A palavra digital também está associada a dígito (do latim digitus de "dedo") que esta associado à representação de quantidades inteiras. Não podemos usar os dedos para representar meio pulso ou um quarto de pulso.
Na eletrônica analógica trabalhamos com quantidades ou sinais que podem ter valores que variam de modo continuo numa escala. Os valores dos sinais não precisam ser inteiros. Por exemplo, um sinal de áudio, que é analógico, varia suavemente entre dois extremos enquanto que um sinal digital só pode variar aos saltos, conforme mostra a figura 1.
Conforme o leitor pode perceber, a diferença básica entre os dois tipos de eletrônica está associada inicialmente ao tipo de sinal com que elas trabalham e no que elas fazem com os sinais.
De uma forma resumida podemos dizer que:
A eletrônica digital trabalha com sinais que só podem assumir valores discretos ou inteiros.
A eletrônica analógica trabalha com sinais que podem ter qualquer valor entre dois limites.
Onde Encontramos A Eletrônica Digital
COMPUTADORES - os computadores atuais são digitais em sua totalidade, e praticamente não se usa outro tipo de configuração, a não ser no interfaceamento com o mundo exterior, pois somos analógicos. No entanto, nem sempre foi assim. Nas primeiras décadas deste século, quando os circuitos eram ainda valvulados os primeiros computadores eram máquinas analógicas. A imprecisão, e algumas outras dificuldades técnicas, que estes computadores apresentavam fizeram com que eles logo fossem substituídos pelos circuitos digitais que nós usamos hoje.
TELECOMUNICAÇÕES - Antigamente também, todos os equipamentos de telecomunicações trabalhavam diretamente com sinais analógicos vindos de microfones, câmeras de TV e outras fontes. No entanto, atualmente a maioria das transmissões de informações sem fio, por ondas de rádio, e por meios físicos como fibras ópticas e cabos, ocorre na forma digital. Os sinais analógicos são convertidos em digitais e, com isso, transmitidos de forma muito mais eficiente.
INDÚSTRIA E AUTOMAÇÃO - Antigamente, os controles de máquinas industriais eram simples, não passando de interruptores e chaves ou, no máximo, dispositivos que controlavam diretamente sinais analógicos. Também neste caso, tivemos uma evolução com o uso de microprocessadores, microcontroladores e DSPs (Digital Signal Processors ou Processadores Digitais de Sinais). Neles, os sinais analógicos de sensores e controle são convertidos em sinais digitais e usados nos equipamentos. Hoje temos a IoT e a Indústria 4.0 que dependem totalmente da eletrônica digital.
INSTRUMENTAÇÃO – A maioria dos instrumentos de laboratório são digitais. Com uma precisão maior e a possibilidade de processar as medidas feitas, eles ainda podem ter recursos para gravar ou enviar dados através da internet ou outros meios de transmissão, com recursos muito maiores do que os equivalentes analógicos.
ELETRÔNICA DE CONSUMO – Muitos dos eletro-eletrônicos que utilizamos hoje possuem chips de controle que nada mais são do que microcontroladores, operando de forma totalmente digital. Isso ocorre com seu aquecedor a gás, seu forno de microondas, seu relógio digital, calculadora, TV, DVD player, e muito mais. Nela incluímos os eletrodomésticos ligados à interne, que leva a IoT.
ELETRÔNICA EMBARCADA –Todos os veículos modernos possuem um microcontrolador que gerencia o funcionamento de suas partes, do motor aos sistemas de segurança e navegação, incluindo-se o GPS e sistemas de entretenimento.
ELETRÔNICA MÉDICA – Uma vasta quantidade de equipamentos médicos utiliza recursos digitais no seu controle, com um grau de sofisticação elevado, pela capacidade dos circuitos empregados. São equipamentos de raios-X, tomografia, etc.

1.2 – Lógica digital
Todos os equipamentos que usam circuitos digitais funcionam obedecendo a um tipo de comportamento baseado no que se denomina Lógica.
Diferentemente dos circuitos amplificadores comuns que simplesmente amplificam, atenuam ou realizam algum tipo de processamento simples dos sinais, os circuitos digitais não processam os sinais baseados em uma finalidade simples que é determinada quando são fabricados.
Os circuitos digitais de todos os equipamentos que fazem uso desta tecnologia são capazes de combinar os sinais, tomando decisões segundo um comportamento lógico.
É evidente que, se o leitor deseja realmente entender as coisas que ocorrem com os circuitos digitais, deve partir exatamente do aprendizado do comportamento que desejamos que eles tenham, ou seja, um comportamento lógico e isso implica em saber que tipo de comportamento é este.
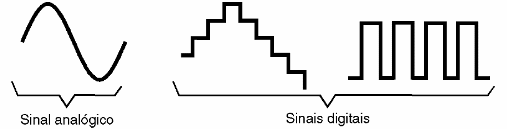
Podemos dizer que a partir da lógica podemos tirar conclusões a partir de fatos conhecidos, ou tomar decisões a partir de fatos conhecidos.
Por exemplo, a decisão de "acender uma lâmpada quando está escuro" é uma decisão lógica, pois a proposição e a conclusão são fatos relacionados.
Ao contrário, a decisão de "acender uma lâmpada porque está chovendo" não é uma decisão lógica, pois os fatos envolvidos não têm relação.
Outros exemplos de lógica:
Acionar um relé quando a temperatura chega a um determinado valor
Tocar uma campainha quando uma peça chegar a uma determinada posição.
Abrir uma porta quando a senha correta for digitada num teclado
As decisões são extremamente simples, mas se combinarmos muitas delas poderemos ter comportamentos muito complexos, como os encontrados nos computadores, máquinas industriais, microcontroladores, robôs, etc.
É claro que estes equipamentos e seus circuitos digitais não podem entender coisas como está escuro ou está chovendo e tomar decisões.
Assim, os circuitos lógicos digitais nada mais fazem do que receber sinais com determinadas características e em sua função tomam decisões que nada mais são do que a produção de outro sinal elétrico.
Mas, se os sinais elétricos são digitais, ou seja, representam quantidades discretas, e se a lógica é baseada em tomada de decisões, o próximo passo no entendimento da eletrônica digital, com sua lógica é justamente partir para o modo como as quantidades discretas são representadas e entendidas pelos circuitos eletrônicos.
1.3 – Sistemas de numeração
O modo como contamos as quantidades vem do fato de possuirmos 10 dedos. Assim, tomando os dedos das mãos, podemos contar objetos com facilidade até certo ponto.
O ponto crítico ocorre quando temos quantidades maiores do que 10. O homem resolveu o problema passando a indicar também a quantidade de mãos, ou de vezes em que os dez dedos são usados.
Assim, quando dizemos que temos 27 objetos, o 2 indica que temos "duas vezes as mãos cheias" ou duas dezenas mais 7 objetos. O 2 tem peso 10.
Da mesma forma, quando dizemos que temos 237 objetos, o 2 agora indica que temos "duas dezenas de pares de mãos cheias" ou duas centenas enquanto que o 3 indica que temos mais 3 pares de mãos cheias e finalmente o 7, mais 7 objetos, conforme mostra a figura 3.
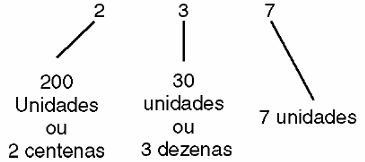
Em outras palavras a posição dos algarismos na representação dos números tem um peso e no nosso sistema de numeração que é decimal esse peso é 10, conforme mostra a figura 4.
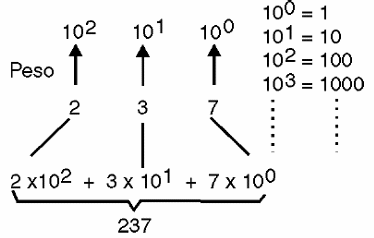
O que aconteceria se tivéssemos um número diferente de dedos, por exemplo, 2 em cada mão?
Isso significaria, em primeiro lugar, que no nosso sistema de base 4 (e não base 10) só existiriam 5 algarismos para representar os números: 0, 1, 2, 3 e 4, conforme mostra a figura 5.
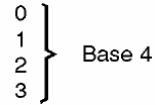
Para representar uma quantidade maior do que 4, teríamos de usar mais de um algarismo.
Assim, para indicar 7 objetos na base 4, teríamos "uma mão cheia com 4" e mais 3. Isso daria 13, conforme mostra a figura 6.
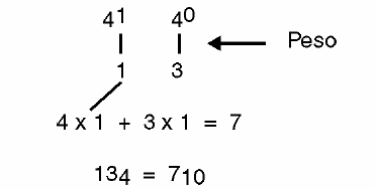
Veja então que no "13" na base 4, o 1 tem peso 4, enquanto que o 3 tem o seu valor normal.
De uma forma generalizada dizemos que, dependendo da base do sistema, os algarismos têm "pesos" que correspondem à sua posição no número, e que estes pesos são potências da base.
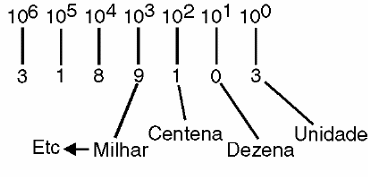
Por exemplo, para a base 10, cada algarismo a partir da direita tem um peso que é uma potência de 10 em ordem crescente, o que nos leva à unidade (10 elevado a 1), à dezena (dez elevado ao expoente 1), à centena (dez elevado quadrado), ao milhar (dez elevado ao cubo) e assim por diante, conforme mostra a figura 7.
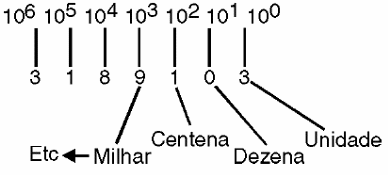
Em eletrônica digital, costumamos dizer que o dígito mais à direita, por representar a menor potência ou ter menor peso, é o dígito (ou bit*) menos significativo ou LSB (Least Signficant Bit), enquanto que aquele que está mais a esquerda é o mais significativo ou MSB (Most Significant Bit).
Para a base 4, os dígitos têm potências de 4 conforme mostra a figura 8.
De qualquer forma, fica até hoje, como herança daqueles povos a divisão do ano em 12 meses, do dia em 12 + 12 horas, das horas em 60 minutos e a própria dúzia
1.4 – Numeração binária
Os circuitos eletrônicos não possuem dedos. É evidente também que não seria muito fácil projetar circuitos que sejam capazes de reconhecer 10 níveis de uma tensão, ou de outra grandeza elétrica, sem o perigo de que, qualquer pequeno problema faça-os o causar confusão.
Uma pequena variação da tensão nestes circuitos pode mudar um 3 para 4 ou vice-versa, afetando os cálculos que ele tenha que realizar.
Muito mais simples para os circuitos eletrônicos é trabalhar com um sistema de numeração que esteja mais de acordo com o seu princípio de funcionamento e isso realmente é feito.
Um circuito eletrônico pode ter ou não ter corrente, pode ter ou não ter tensão, pode receber ou não um pulso elétrico.
Também é muito mais fácil diferenciarmos dois estados de elementos indicadores como uma lâmpada acesa ou apagada, uma campainha em silêncio ou tocando.
Ora, os circuitos eletrônicos são mais apropriados para operar com sinais que tenham duas condições possíveis, ou seja, que representem dois dígitos ou algarismos.
Também podemos dizer que as regras que regem o funcionamento dos circuitos que operem com apenas duas condições possíveis são muito mais simples.
Assim, o sistema adotado nos circuitos eletrônicos digitais modernos é o sistema binário ou de base 2 onde apenas dois dígitos são usados, correspondentes a duas condições possíveis de um circuito: 0 e 1.
Mas, como podemos representar qualquer quantidade usando apenas dois algarismos?
A ideia básica é a mesma usada na representação de quantidades no sistema decimal: atribuir pesos aos dígitos conforme sua posição no número.
Para entendermos melhor como tudo isso funciona, vamos tomar como exemplo o valor 1101 que em binário representa o número 13 decimal (*) e ver como isso ocorre.
(*) Para não fazermos confusões em relação ao tipo de base que está sendo usada para representar um número ou quantidade, é comum colocarmos ao lado, como índice, a base que está sendo usada.
Assim, ao falarmos em 1101 em binário, escrevemos simplesmente 11012 e para representar 13 em decimal, escrevemos 1310 .Esta forma de indicarmos as bases de um número, será adotada em nossas lições daqui por diante.
O primeiro dígito da direita nos indica que temos uma vez o peso deste dígito ou 1. O zero do segundo dígito da direita para a esquerda, indica que não temos nada com o peso 2. Agora o terceiro dígito da direita para a esquerda, e que tem peso 4, é um 1, o que indica que temos "uma vez quatro". Finalmente o primeiro dígito da esquerda que é um 1, e que está na posição de peso 8, nos diz que temos "uma vez oito".
Somando uma vez oito, com uma vez quatro e uma vez um, temos o total que é justamente a quantidade que conhecemos em decimal como treze.
Veja então que, conforme mostra a figura 9, na numeração binária, os dígitos vão tendo pesos, da direita para a esquerda que são potencias de 2, ou seja, dois elevado ao expoente zero que é um, dois elevado ao expoente 1 que é 2; dois ao quadrado que é 4 e assim por diante.
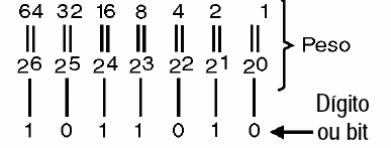
Para o leitor, basta lembrar que a cada dígito que nos deslocamos para a esquerda, seu peso dobra, conforme mostra a figura 10.
Como não existe um limite para os valores dos pesos, isso significa que é possível representar qualquer quantidade em binário, por maior que seja, simplesmente usando a quantidade apropriada de dígitos.
Para 4 dígitos podemos representar números até 15; para 8 dígitos podemos ir até 255; para 16 dígitos podemos ir até 65 535 e assim por diante.
O leitor deve lembrar-se desses valores limites para 4, 8, 16 e 32 dígitos de um número binário, pois eles têm uma grande importância nas aplicações digitais modernas.
A seguir damos a representação binária dos números decimais até 17 para que o leitor tenha uma ideia de como tudo funciona:
| decimal | binário | decimal | binário | |
| 0 | 0 | 9 | 1001 | |
| 1 | 1 | 10 | 1010 | |
| 2 | 10 | 11 | 1011 | |
| 3 | 11 | 12 | 1100 | |
| 4 | 100 | 13 | 1101 | |
| 5 | 101 | 14 | 1110 | |
| 6 | 110 | 15 | 1111 | |
| 7 | 111 | 16 | 10000 | |
| 8 | 1000 | 17 | 10001... |
Para o leitor que pretende entender de eletrônica digital aplicada aos computadores, equipamentos industriais, médicos e muitos ouros existem momentos em que é preciso saber converter uma indicação em binário para o decimal correspondente.
Podemos dar como exemplo o caso de certas placas que são usadas no diagnóstico de computadores e de máquinas industriais as quais possuem um conjunto de LEDs que acendem indicando um número correspondente a um código de erros.
Os LEDs apagados indicam o algarismo 0 e os LEDs acesos indicam o algarismo 1, conforme mostra o exemplo da figura 11, em que temos uma placa com um display e um conjunto de 4 LEDs para indicação em binário.

Vamos supor que num diagnóstico a sequência de acendimento dos LEDs seja 1010. De início o leitor precisa saber por onde começar a leitura, ou seja, se o de menor peso é o da direita ou da esquerda.
Nas indicações dadas por instrumentos ou mesmo na representação da valores binários como, por exemplo, na saída de um circuito é preciso saber qual dos dígitos tem maior peso e qual ter menor peso.
Isso é feito com uma sigla que é adotada normalmente e que refere-se ao dígito, no caso denominado bit.
Assim, para o dígito de menor peso ou bit menos significativo é adotada a sigla LSB (Least Significante Bit) e para o mais significativo é adotada a sigla MSB (Most Significant Bit), conforme mostra a figura 12.

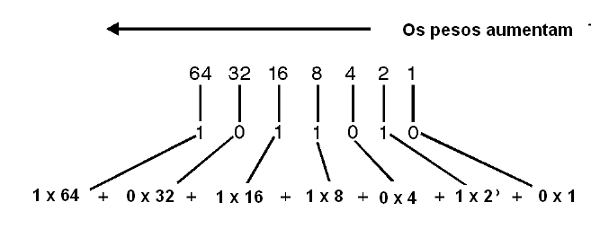
O que fazemos é somar os valores dados pelos dígitos multiplicados pelo peso de sua posição. No caso do valor tomado como exemplo, 1010110, temos:
| Dígito | Peso | Valor |
| 1 | x 64 | = 64 |
| 0 | x 32 | = 0 |
| 1 | x 16 | = 16 |
| 0 | x 8 | = 0 |
| 1 | x 4 | = 4 |
| 1 | x 2 | = 2 |
| 0 | x 1 | = 0 |
Somando os valores temos:
64 + 16 + 4 + 2 = 86
O valor decimal de 1010110 é 86, ou usando a notação mais apropriada:
10101102 = 8610
Observe que, para fazer uma conversão, tudo que o leitor tem de fazer é lembrar que a cada dígito que saltamos para a esquerda seu peso dobra na sequência 1, 2, 4, 8, 16, 32, 64, 128, etc.
Na prática, também pode ocorrer o problema inverso que é a transformação de um valor expresso em decimal (base 10) para a base 2 ou binário.
Para esta transformação podemos fazer uso de algoritmo muito simples que memorizado pelo leitor pode ser de grande utilidade, dada sua praticidade.
Vamos ver então como usar o algoritmo para a conversão de um decimal para binário como, por exemplo, o 116. O que fazemos é uma série de divisões sucessivas, conforme mostra a figura 13.
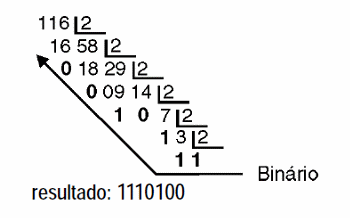
Veja então que vamos dividindo os números por 2 até o ponto em que chegamos a um valor menor que 2 e que, portanto, não mais pode ser dividido.
O resultado desta última divisão, ou seja, seu quociente é então o primeiro dígito binário do número convertido. Os demais dígitos são obtidos lendo-se os restos da direita para a esquerda da série de divisões que realizamos. Tudo muito simples e rápido.
1.4.1 - Quilo, Mega e Giga
Em eletrônica digital, assim como na eletrônica analógica tradicional é comum o uso de prefixos para representar quantidades muito grandes ou muito pequenas.
Dessa forma, os prefixos Quilo (k) para representar milhares, Mega (M) para representar milhões e Giga (G) para representar bilhões também são usados em eletrônica digital.
No entanto, diferentemente, do que ocorre com a eletrônica analógica, esses prefixos representam quantidades "levemente" diferentes.
O que ocorre é que quando usamos quilo (k) para representar 1 000 (mil), na base 10, 1000 é um valor inteiro, o que não ocorre com a base 2.
Assim, o valor mais próximo da base 2 é 1024. Isso significa que, em eletrônica digital, o valor quilo, na realidade representa 1024. Uma memória que tenha uma capacidade de armazenar 1 quilo bit ou 1 kb, na verdade, armazena 1024 bits.
Da mesma forma, quando falamos que um programa de computador exige um espaço de memória de 1 Mega bytes, na verdade, ele exige um espaço de 1 048 576 bytes, já que a potência de 2 mais próxima de 1 milhão é 1 048 576.
1.5 – Binários menores que 1
Para o leitor, talvez seja difícil entender como usando quantidades que só podem ser inteiras, como dado pela definição de digital no início desta lição, seja possível representar quantidades menores que um, ou seja, números "quebrados" ou fracionários.
É claro que isso é possível na prática, pois se assim não fosse os computadores, equipamentos digitais de controle e automação e as calculadoras não poderiam realizar qualquer operação com estes números e sabemos que isso não é verdade.
O que se faz é usar um artifício que consiste em empregar potências negativas de um número inteiro, para representar quantidades que não são inteiras. Desta forma, é possível usar dígitos binários para representar quantidades fracionárias sem problemas.
Vamos dar um exemplo tomando como exemplo o número 0,01101 em binário .
A própria existência de um "0," já nos sugere que se trata de um número menor que 1 e portanto fracionário.
O que ocorre é que os dígitos deste número têm pesos que correspondem à potências de 2 negativas, e que nada mais são do que frações, conforme a seguinte sequência:
| Dígito | Peso | Valor |
| 0, | x 1 | 0 |
| 0 | x | 1/2 0,5 |
| 1 | x 1/4 | 0,25 |
| 1 | x 1/8 | 0,125 |
| 0 | x 1/16 | 0,0625 |
| 1 | x 1/32 | 0,03125 |
Somando os valores relativos temos:
0,25 + 0,0625 + 0,03125 = 0,625
O número decimal representado é, portanto, 0,625.
1.5.1 - Potências Negativas de 2
Na tabela dada a seguir temos algumas potências negativas de 2, usadas para representar números menores que 1.
Potência Negativa de 2 Decimal
20 1
2-1 0,5
2-2 0,25
2-3 0,125
2-4 0,062 5
2-5 0,031 25
2-6 0,015 625
2-7 0,007 812 5
2-8 0,003 906 25
2-9 0,001 953 125
2-10 0,000 976 562 5
2-11 0,000 488 281 25
2-12 0,000 244 140 625
2-13 0,000 122 070 312 5
2-14 0,000 061 035 156 25
2-15 0,000 030 517 578 125
1.6 – Formas diferentes de usar o sistema binário
A utilização de circuitos eletrônicos com determinadas características, e a própria necessidade de se adaptar o sistema binário à representação de valores que sejam convertidos rapidamente para o decimal, e mesmo outros sistemas, levou ao aparecimento de algumas formas diferentes de utilização dos binários denominados "puros".
Estas formas são encontradas em diversos tipos de equipamentos digitais incluindo os próprios computadores.
1.6.1 - Sistema BCD (Decimal Codificado em Binário)
BCD é a abreviação de Binary Coded Decimal e se adapta melhor aos circuitos digitais por características que ficarão mais claras no decorrer de nosso curso.
O que se faz é transformar cada dígito decimal de um número em um grupo de quatro dígitos binários (bits) independentemente do valor total do número que vai ser representado.
Assim, partimos da seguinte tabela:
| Dígito decimal | BCD |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
Assim, se quisermos representar em BCD o número 23,25 não o convertemos da forma convencional por divisões sucessivas mas sim, tomamos cada dígito decimal e o convertemos no BCD equivalente conforme se segue:
| 2 | 3 | 2 | 5 |
| 0010 | 0011 | 0010 | 0101 |
Veja então que, para cada dígito decimal sempre teremos quatro dígitos binários ou bits e também que os valores 1010, 1011, 1100, 1101 e 1111 não existem neste código.
Esta representação foi muito interessante quando as calculadoras se tornaram populares, pois podia ser usada para todas as operações com números comuns e os 5 códigos que não eram usados dos valores que não existiam forem adotados para indicar as operações! (figura 14)
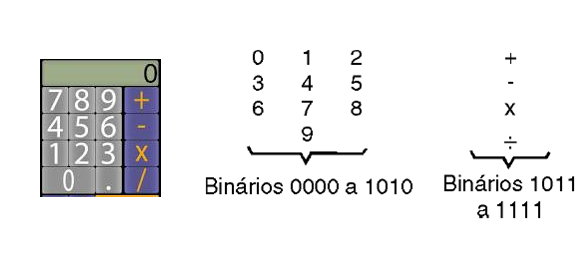
Usando representações desta forma, operavam os primeiros computadores que muito apropriadamente eram chamados de computadores de "4 bits".
1.6.2 – Código Biquinário
Existem diversos outros códigos utilizados em equipamentos eletrônicos digitais que merecem destaque. Outro deles é o Código Biquinário.
Neste código temos 7 bits com pesos diferentes. Os dois primeiros bits ou dígitos, indicam se o número está entre 0 e 5 ou entre 5 e 9.
Por exemplo, se o número é 7, temos nos dois primeiros bits 1 e 0, pois o número é maior que 5. Os outros bits indicam, quanto deve ser somado ao 5 para se obter o 7. Assim, usamos o bit de peso 2 para esta finalidade pois:
5 + 7 = 7
Temos então como representação do valor 7 neste código
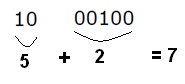
A tabela abaixo nos dá as representações dos decimais de 0 a 9 neste código.
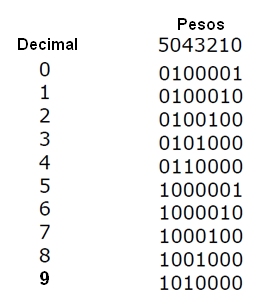
1.6.3 – Código Excesso 3 (XS3)
Podemos dizer que se trata de uma variação do BCD. Nele, a diferença é que a cada dígito representado, é acrescentado 3 ao valor correspondente em BCD, conforme a seguinte tabela.
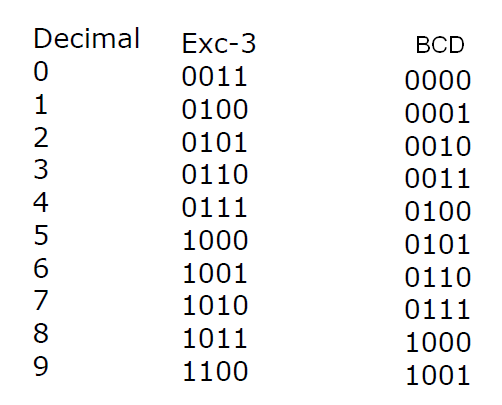
Veja então que, para representar o valor 5, somamos 3, e com isso, usamos o BCD 8 (1000).
A vantagem do uso deste código está na facilidade com que ele pode ser usado em operações matemáticas.
1.6.5 – Código Gray
O código Gray se caracteriza pelo fato da passagem de qualquer número para o seguinte sempre ser feita com a mudança de um único dígito.
Assim, por exemplo, quando passamos de 0111 (7 em decimal) para 1000 (8 em decimal) os quatro dígitos mudam. No código gray a passagem do 7 para 8 muda apenas um dígito pois o 7 ‚ 0100 e o 8 ‚ 1100.
A vantagem da mudança de apenas um dígito, na passagem de um número para o seguinte (ou volta ao anterior), está na possibilidade de se ter maior velocidade dos circuitos e menor consumo. Conforme veremos nas próximas lições, o consumo de um circuito digital ocorre na maior parte, no momento em que ele realiza uma operação lógica, ou seja, muda de estado.
Uma aplicação deste código está nos encoders ópticos, que são dispositivos ópticos em que se tem uma codificação através de zonas claras e escuras que permitem medir sua velocidade de rotação, ou ainda determinar sua posição, conforme mostra a figura 15.
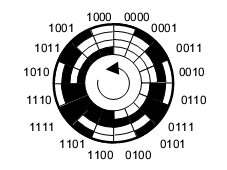
Na tabela abaixo temos alguns valores decimais, e os correspondentes binários e no código Gray.
|
Decimal |
Binário |
Gray |
|
0 |
0000 |
0000 |
|
1 |
0001 |
0001 |
|
2 |
0010 |
0011 |
|
3 |
0011 |
0010 |
|
4 |
0100 |
0110 |
|
5 |
0101 |
0111 |
|
6 |
0110 |
0101 |
|
7 |
0111 |
0100 |
|
8 |
1000 |
1100 |
|
9 |
1001 |
1101 |
|
10 |
1010 |
1111 |
|
11 |
1011 |
1110 |
|
12 |
1100 |
1010 |
|
13 |
1101 |
1011 |
|
14 |
1110 |
1001 |
|
15 |
1111 |
1000 |
1.6.6 – Código 987654321
No código 9876543210, temos uma decodificação de "uma saída de 10", ou seja, um único bit será 1 enquanto os demais serão 0, conforme o dígito a ser representado, conforme a seguinte tabela:
|
Decimal |
9876543210 |
|
0 |
0000000001 |
|
1 |
0000000010 |
|
2 |
0000000100 |
|
3 |
0000001000 |
|
4 |
0000010000 |
|
5 |
0000100000 |
|
6 |
0001000000 |
|
7 |
0010000000 |
|
8 |
0100000000 |
|
9 |
1000000000 |
A desvantagem deste código está no fato de precisarmos de 8 bits para representar os dígitos de 0 a 9.
1.6.7 - ASCII
Temos também códigos mais complexos como o ASCII (American Standard Code for Information Interchange), muito usado em informática.
Levando em conta que, com 8 bits podemos representar 256 valores diferentes, foi criado um código de 8 bits que correspondem aos principais símbolos (letras, números, sinais de pontuação, etc.) mais utilizados num sistemas de comunicações.
Assim, quando usamos o teclado do computador, a cada tecla está associado um byte correspondente a este código, o qual é decodificado e enviado ao computador. O mesmo ocorre, quando selecionamos uma tecla de letra, número ou outro símbolo gráfico no teclado do telefone celular, para digitar uma mensagem. Desta forma, quando digitamos a letra A, o byte enviado é 0100 0001.
Nesta tabela temos ainda a indicação dos valores correspondentes em binário no sistema de numeração base 16, ou hexadecimal, que estudaremos mais adiante.
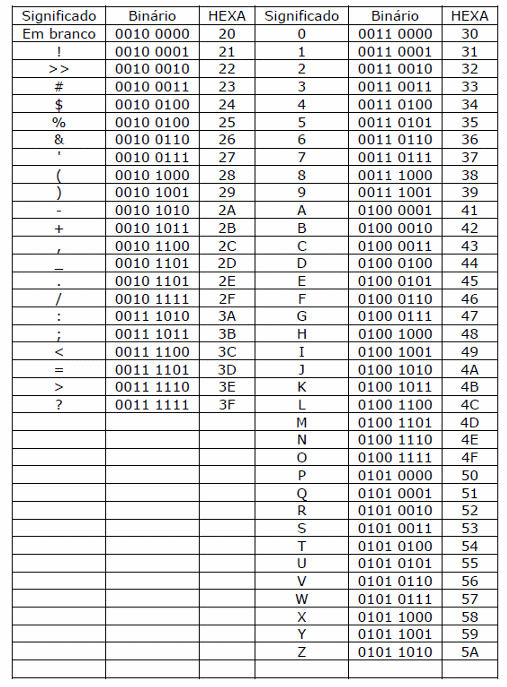
Esta tabela contém os 128 primeiros códigos, havendo uma extensão para os códigos até 256.
Veja que nesta tabela também temos a indicação do símbolo em hexadecimal (hex) que é outro sistema que estudaremos no item 1.7, pela sua importância.
1.6.8 – Código Fortran
Nos primeiros computadores digitais, os programas eram digitados e passados a cartões perfurados do tipo Hollerith. Cada linha do programa correspondia a um cartão que depois eram empilhados consistindo assim no programa completo.
Levados a uma leitura, estes cartões eram “puxados” um a um para seu interior, onde depois de lidos, rodavam o programa apresentando o resultado numa folha impressa.
Na figura 16 temos um exemplo desses cartões perfurados com o código usado.

1.6.9 - Códigos de erros
Na transmissão de dados na forma digital, é de extrema importância garantir a integridade da informação. Para esta finalidade existem recursos que permitem saber se um número na forma binária foi transmitido corretamente ou não. Para isso são agregados códigos especiais, denominados códigos de erro.
1.6.10 – Binário com Paridade
Uma maneira de simples de se detectar a integridade de um valor binário transmitido em BCD consiste em se acrescentar um bit que indique a paridade. Assim, esse bit será 1, se a soma dos bits dos quatro bits transmitidos for impar e será 0, se a soma for par. Como exemplo, damos dois casos possíveis, onde p é o bit de paridade.

Neste código existem sempre dois dígitos 1, conforme a seguinte tabela:

Desta forma, se numa transmissão de dados, aparecer um bloco de 5 bits com um número diferente de 2 de bits 1, então pode-se saber que os dados chegaram de forma incorreta.
1.7 - SISTEMA HEXADECIMAL
Os bits dos circuitos digitais são agrupados em conjuntos de 4, assim (nibble), desta forma temos os microprocessadores e computadores de 4, 8, 16 e 32 bits, etc.
Também observamos que, com 4 bits podemos obter representações binárias de 16 números, e não somente de 10. Vimos que os 5 excedentes poderiam ser usados para representar operações nas calculadoras.
Isso significa que, muito mais compatível com a numeração binária ou operação binária dos circuitos digitais, como os computadores, é a representação de valores no sistema hexadecimal ou de base 16.
E, de fato isso é feito: abrindo muitos programas de um computador vemos que suas características como posições de memória ou quantidade de memória são feitas neste sistema.
Isso significa que todos que trabalham com eletrônica digital precisam conhecer este sistema e, mais do que isso, saber como fazer conversões dele para o decimal e vice-versa além de conversões para o sistema binário.
Na tabela abaixo damos as representações dos dígitos deste sistema tanto com equivalentes decimais como binários:
| Decimal | Binário | Hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Na figura 16 temos a apresentação dos valores de 0 a 15 em displays de 7 segmentos, utilizando a codificação hexadecimal.

Observe que, como não existem símbolos para de dígitos para 10,11,12,13,14 e 15, foram usadas as letras A,B,C,D,E e F.
Como fazer as conversões: os mesmos procedimentos que vimos para o caso das conversões de decimal para binário e vice-versa são válidos para o caso dos hexadecimais mudando-se apenas a base.
Como converter 4D5 em decimal:
Os pesos no caso são: 256, 16 e 1. (a cada dígito para a esquerda multiplicamos o peso do anterior por 16 para obter novo peso).
Temos então:
4D5 = (4 x 256) + (13 x 16) + (1 x 5) = 1237
Observe que o "D" corresponde ao 13. O número decimal equivalente ao 4D5 hexadecimal ou "hex" como é muitas vezes representado, é 1237.
4D5 (hex) = 1237 (dec)
A conversão inversa, ou seja, de decimal para hexadecimal é feita por divisões sucessivas. Tomemos o caso de 1256, mostrado na figura 17.
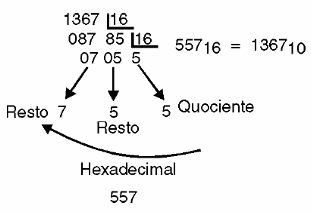
Veja então que basta ler o quociente final e depois os restos das divisões sucessivas, sempre lembrando que os que excederem 10, devem ser "trocados" pelas letras equivalentes.
1.8 – Aritmética Binária
Da mesma forma que podemos realizar operações com números decimais, podemos também somar, subtrair, multiplicar ou dividir números binários.
Para trabalhar com números binários os procedimentos (algoritmos) são bastante semelhantes aos usados com os números decimais e, evidentemente, podemos aplicar estes procedimentos a números em qualquer base.
Para realizar operações aritméticas com números binários basta lembrar algumas regras básicas que são dadas a seguir:
As operações com números binários seguem certas regras que são dadas a seguir:
a ) Soma:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (vai um)
b) Subtração:
0 - 0 = 0
0 - 1 = 1 (empresta 1)
1 - 0 = 1
1 - 1 = 0
c) Multiplicação:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
d) Divisão:
0 : 0 = 0
0 : 1 = 0
1 : 0 = não permitido
1 : 1 = 1
Vamos tomar como exemplo a soma binária de 6 (0110) com 7 (1110). Colocando um número sobre o outro, como na figura 18 (a).
Somando a última coluna da direita, seguindo as regras dadas acima, temos que 0 + 1 = 1 e “vai 0” para ser transportado para a segunda coluna, como mostra a figura 18 (b)
A seguir somamos os três dígitos da segunda coluna: 0 + 1 + 1 = 1 e “vai 1”, que é transportado para a terceira coluna, como vemos na figura 18 (c).
Somamos agora os três dígitos da terceira coluna 1 + 1 + 1 = 1 e “vai 1”, que é transportado para a quarta coluna, conforme mostra a figura 18 (d).
Finalmente somamos os dígitos da quarta coluna: 1 + 0 + 0 = 1 e “vai 0”. Com isso chegamos resultado final na figura 18(e)
É fácil então converter 1101, que é o resultado final, em decimal, chegando ao resultado esperado: 13.
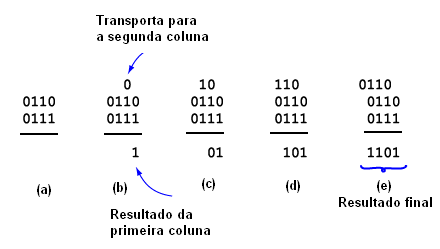
Um exemplo de subtração binária é dado a seguir. Observe que na primeira coluna, como não podemos tirar 1 de 0, “emprestamos 1” da segunda coluna (da direita para a esquerda), exatamente como fazemos com os números decimais. Na figura 19 temos um exemplo de subtração binária.
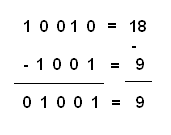
Para a multiplicação, podemos dar o seguinte exemplo, observando, que da mesma forma que na multiplicação decimal, multiplicamos os números da primeira linha por cada um da segunda linha, conforme mostra a figura 20.
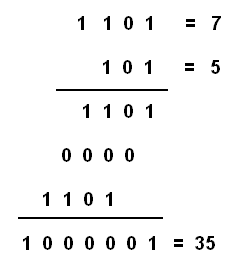
Finalmente podemos dar um exemplo de divisão binária na figura 21:
Índice
Curso de Eletrônica Digital – Analógica e Digital – Sistemas de Numeração (CUR5001)
Curso de Eletrônica Digital – A Álgebra de Boole (CUR5002)
Curso de Eletrônica Digital – Famílias de Circuitos Lógicos Digitais (CUR5003)
Curso de Eletrônica - Eletrônica Digital – A Família de Circuitos Integrados CMOS (CUR5004)
Curso de Eletrônica Digital – Combinando Funções Lógicas - (Lógica Combinacional) (CUR5005)
Curso de Eletrônica - Eletrônica Digital - Os Elementos Biestáveis (CUR5006)
Curso de Eletrônica - Eletrônica Digital - Flip-Flops e Funções Integradas em CIs (CUR5007)
Curso de Eletrônica - Eletrônica Digital - Os Multivibradores Astáveis e Monoestáveis (CUR5008)
Curso de Eletrônica - Eletrônica Digital - Os Contadores Digitais (CUR5009)
Curso de Eletrônica - Eletrônica Digital - Memórias, ADCs e DACs (CUR5013)